Main results
Week 3: From Naive Bayes to Neural Networks
Dr. Philipp K. Masur
Machine learning is the study of computer algorithms that can improve automatically through experience and by the use of data
The field originated in an environment where the available data, statistical methods, and computing power rapidly and simultaneously evolved
Due to the “black box” nature of the algorithm’s operations, it is often seen as a form of artificial intelligence
Source: qlik
 Applying machine learning in practical context:
Applying machine learning in practical context:
What is Machine Learning?
1.1. Concepts and Principles
1.2. The General Machine Learning Pipeline
1.3. Difference between statistics and machine learning
1.4. Over- vs. underfitting
1.5. Training vs. Testing
1.6. Example Data: Predicting Genre from Lyrics
Supervised text classification with different “algorithms”
2.1. Naive Bayes
2.2. Logistic Regression
2.3. Support Vector Machines
2.4. Artificial Neural Networks
Testing Different Approaches
3.1. Performance of different approaches
3.2. Fine-tuning preprocessing and hyperparameters
3.3. Effect of text preprocessing
3.4. Validity of different text classification approaches
Examples from the Literature
4.1. Incivility on Facebook (Su et al., 2018)
4.2. Electoral News Sharing (de León et al., 2021)
Summary and Conclusion
In the previous lecture, we talked about deductive approaches (such as dictionary approaches)
These are deterministic and are based on a priori text theory (e.g., happy -> positive, hate -> negative)
Yet, natural language is often ambiguous and a probabilistic coding may be better
Dictionary-based or generally rule-based approaches are not very similar to manual coding; a human being assesses much more than just a list of words
Inductive approaches promise to combine the scalability of automatic coding with the validity of manual coding (supervised learning) or can even identify things or relations that we as human beings cannot identify (unsupervised learning)
The general goal, however, is always the same: Model the relationship between…
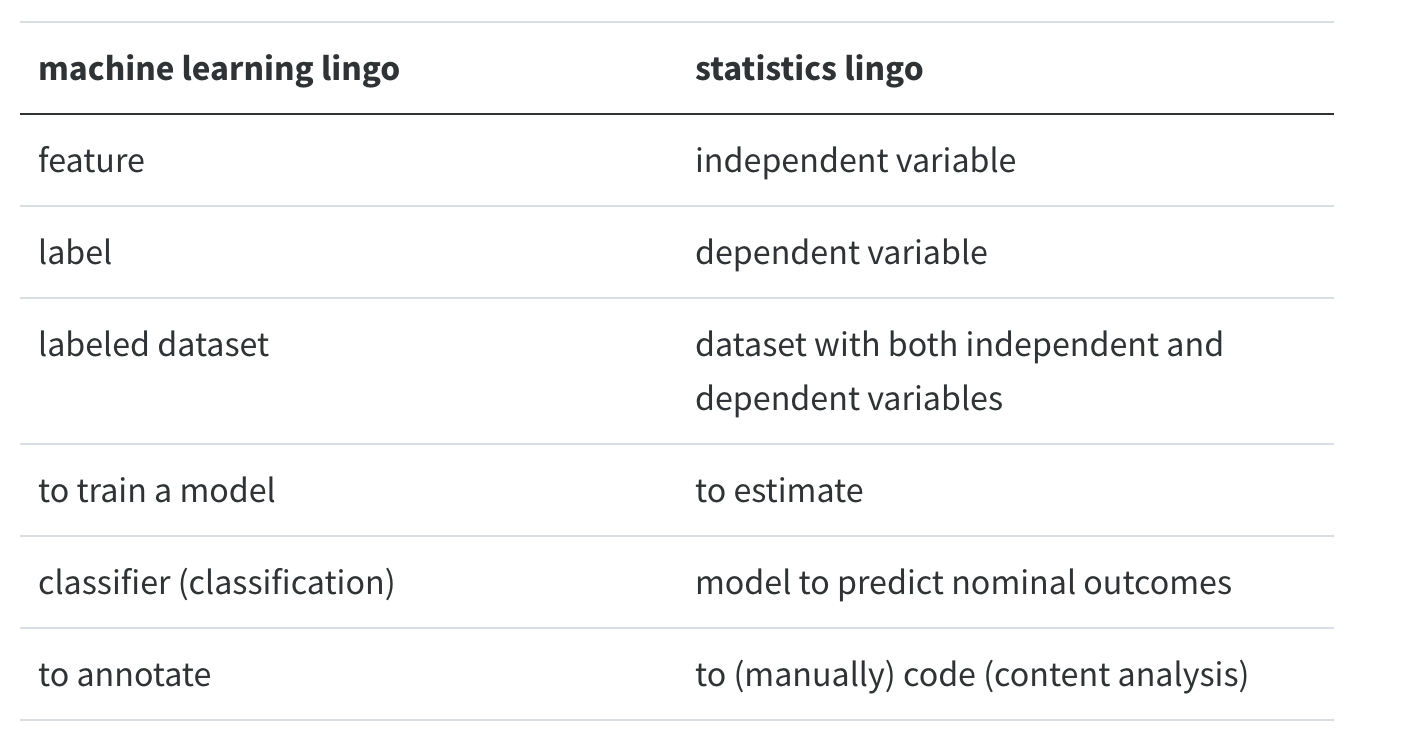
Machine learning, many people joke, is nothing other than a fancy name for statistics.
There is some truth to this: if you say “logistic regression”, this will sound familiar to both statisticians and machine learning practitioners.
Still, there are some differences between traditional statistical approaches and the machine learning approach, even if some of the same mathematical tools are used.

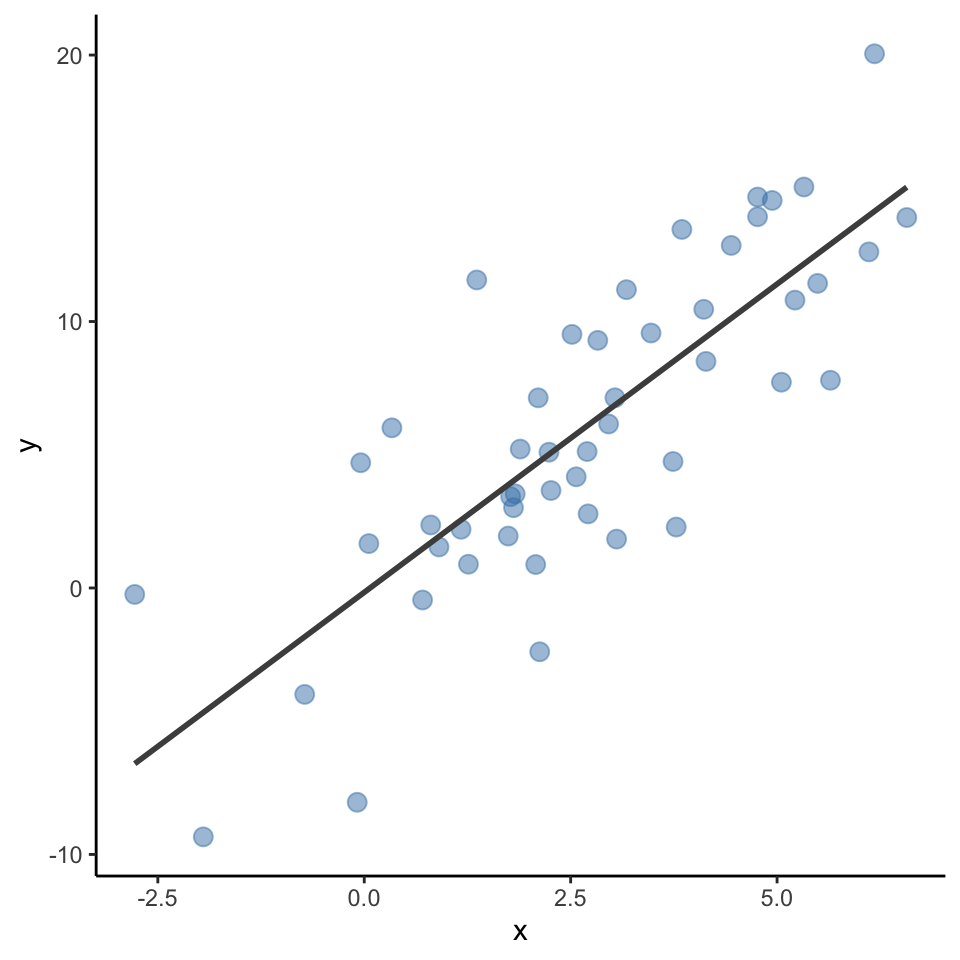
Statistical modeling is about understanding the relationship between one (or several predictors) and an outcom variable
Learn \(f\) so you can predict \(y\) from \(x\):
y based on x:x increases by one unit,y increases by 2.31 units.
Machine learning is less about understanding the relationship, but about maximizing prediction.
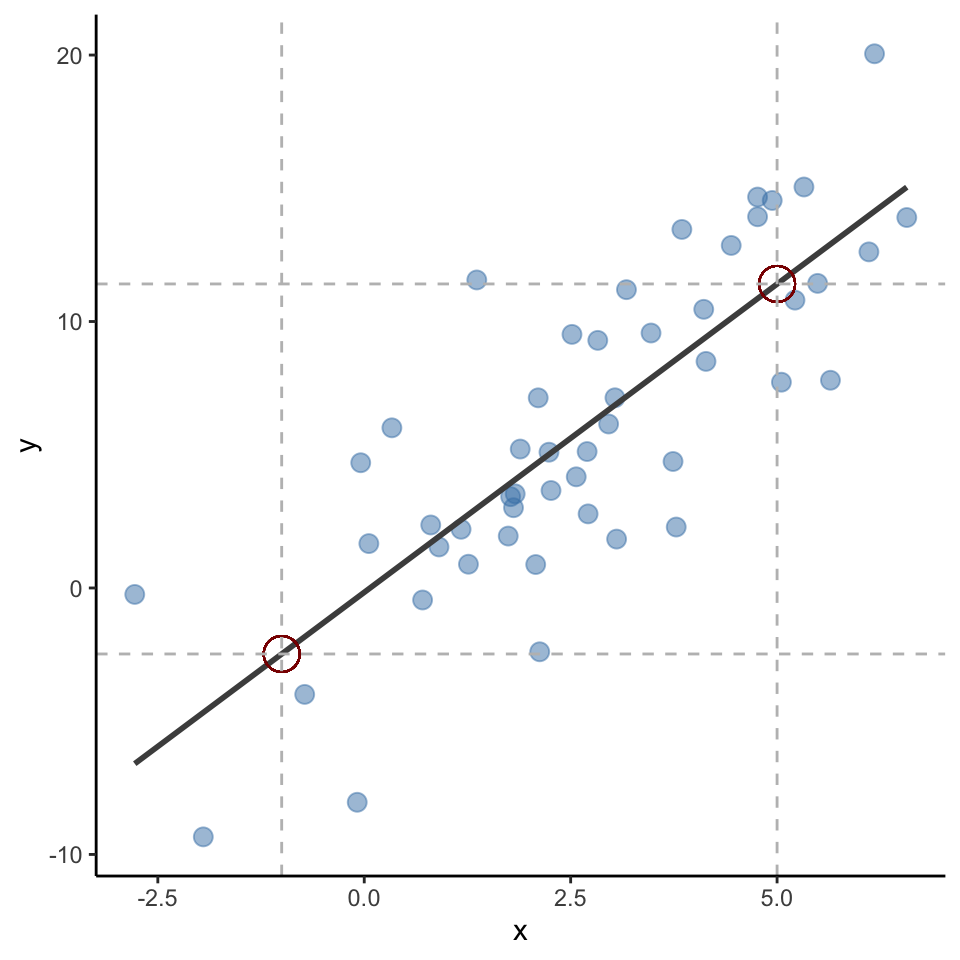
A statistical model such as the one estimated can be used to predict most likely y values based on new x data.
For example, despite not being in the data, x = -1 should be y = -2.47; x = 5 should be y = 11.41 based on the fitted line!
In other words, machine learnings doesn’t focus on explanation, but emphasizes prediction.
Goal of statistical modeling: explaining/understanding
Goal of machine learning: best possible prediction
Note: Machine learning models often have 1000’s of collinear independent variables and can have many latent variables!
Problem in Machine Learning: Sufficiently complex algorithms can “predict” all training data perfectly
But such an algorithm does not generalize to new data (the actual goal!)
Essentially, we want the model to have a good fit to the data, but we also want it to not optimize on things that are specific to the training data set
Problem of under- vs- overfit
Regularization during fitting process
Out-of-sample validation
In sum, we need to validate our new classifier on unseen data
As models (almost) always overfit, it is clear that performance on only training data is not a good indicator of the real quality of the classifier
The standard solution is to split the labeled data into a training and test data sets: This way, we can train the algorithm on one part and then evaluate its validity / performance on the held-out part of the data.
We prevent overfit if the classifier still perform well on unseen data and not just on the training data!
Remember how we validated dictionary approaches?
In supervised text classification, the procedure is similar
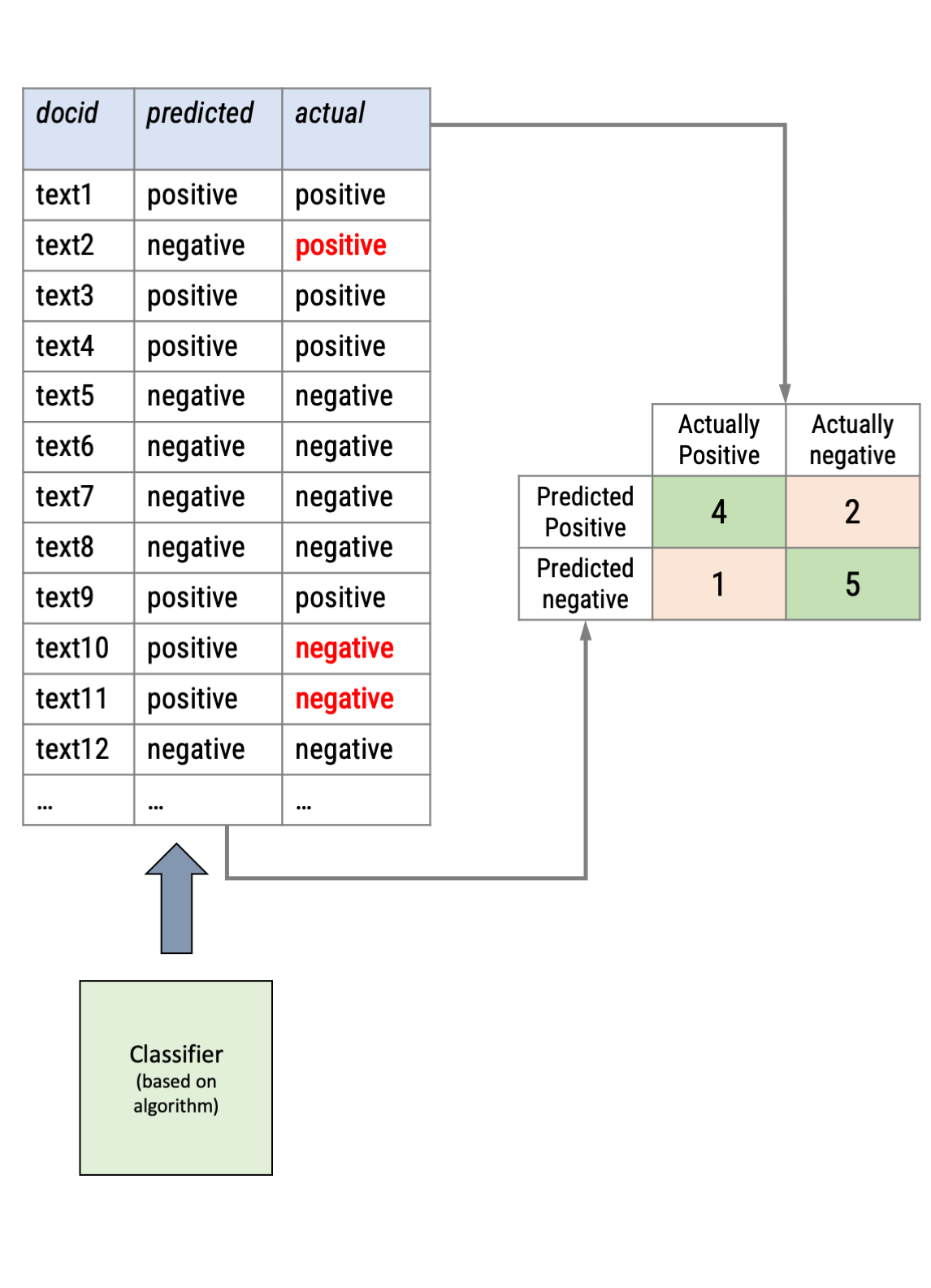
Many aspects of machine learning are non-deterministic, i.e., there is a certain randomness in the procedure
Problem: Research thereby becomes not replicable and the outcome may be affected
To ensure replicability
set.seed(123)For valid outcome:
For the remainder of this lecture, I will exemplify different approaches to supervised text classification using a data set that contains song lyrics and the genre of the artist.
The goal is to investigate whether we can train an algorithm sufficiently well to predict the genre from only song lyrics.
library(tidyverse)
# Set seed
set.seed(42)
# Read data
lyrics_data <- read_csv("data/lyrics-data-prep.csv") |>
mutate(binary_genre = factor(ifelse(Genre =="Rock","rock", "other"), # <-- create binary outcome
levels = c("rock", "other") )) |> # <-- order categories!
sample_frac(size = .20) |> # <-- Sample 20% of the data
select(doc_id = SLink, Artist, Song = SName,
Genre, binary_genre, text = Lyric)
head(lyrics_data)# A tibble: 6 × 6
doc_id Artist Song Genre binary_genre text
<chr> <chr> <chr> <chr> <fct> <chr>
1 /snoop-dogg/213-tha-gangsta-clicc.html Snoop Dogg 213 Tha Gangsta Clicc Hip … other "[Sn…
2 /far-east-movement/jello-feat-rye-rye.html Far East Movement Jello (feat. Rye Rye) Pop other "Jel…
3 /janet-jackson/got-till-its-gone.html Janet Jackson Got 'til It's Gone (feat. Q-Tip… Pop other "Wha…
4 /tori-amos/yo-george.html Tori Amos Yo George Rock rock "I s…
5 /van-morrison/a-sense-of-wonder.html Van Morrison A Sense of Wonder Rock rock "I w…
6 /heart/together-now.html Heart Together Now Rock rock "Dee…This data is scraped from the “Vagalume” website, so it depends on their storing and sharing millions of song lyrics (not really representative or complete)
Contains artist name, song name, lyrics, and genre of the artist (not the song)
The following genres are in this subsample of the data set:
library(tidytext)
lyrics_data |>
filter(Artist == "Radiohead" & Song == "Paranoid Android") |>
unnest_tokens(lines, text, token = "sentences") |>
select(lines) |>
print(n = 20)# A tibble: 39 × 1
lines
<chr>
1 please could you stop the noise, i'm trying to get some rest.
2 from all the unborn chicken voices in my head.
3 what's this...?
4 (i may be paranoid, but not an android).
5 what's this...?
6 (i may be paranoid, but not an android).
7 when i am king, you will be first against the wall.
8 with your opinion which is of no consequence at all.
9 what's this...?
10 (i may be paranoid, but no android).
11 what's this...?
12 (i may be paranoid, but no android).
13 ambition makes you look pretty ugly.
14 kicking and squealing gucci little piggy.
15 you don't remember.
16 you don't remember.
17 why don't you remember my name?.
18 off with his head, man.
19 off with his head, man.
20 why don't you remember my name?.
# ℹ 19 more rows
There are different way to think about creating a test vs. training data set
Simplest form: split-half (or any other percentage distribution)
But there are also other, more complex procedures that fall under the term “cross-validation”
What approach is meaningful depends on the question and goal!


For the entire model fitting process, we are going to use the package tidymodels, which nicely intersects with the already known package tidytext
Here, we can use the functions initial_split to split our data set. The functions training and testing create the actual data sets from the splits.
library(tidymodels)
# Set seed to insure replicability
set.seed(42)
# Create initial split proporations
split <- initial_split(lyrics_data, prop = .60)
# Create training and test data
train_data <- training(split)
test_data <- testing(split)
# Check
tibble(dataset = c("training", "testing"),
n_songs = c(nrow(train_data), nrow(test_data)))From Logistic Regression to Neural Networks.
Classic machine learning models require a numerical representation of text (e.g., document-feature matrix)
They further need the outcome variable that they should predict
All text-preprocessing steps (e.g., stopword removal, stemming, lemmatization, frequency trimming, weighting, etc.) may change the performance, but no clear rules on what works and what does not
Only solution: Trial and error!
library(tidytext)
# Text Preprocessing
dfm_train <- train_data |>
unnest_tokens(word, text) |>
anti_join(stop_words) |>
group_by(doc_id, word) |>
summarize(n = n()) |>
pivot_wider(names_from = word, values_from = n, values_fill = 0)
# Check
dfm_train |> head()# A tibble: 6 × 43,613
# Groups: doc_id [6]
doc_id answer blowing breeze brick burning candle changed close color considered distant earth fading fingers flowers
<chr> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
1 /10000… 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1
2 /10000… 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0
3 /10000… 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 /10000… 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 /10000… 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0
6 /10000… 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# ℹ 43,597 more variables: forever <int>, frozen <int>, funny <int>, glass <int>, grey <int>, hold <int>, home <int>,
# lane <int>, liquid <int>, live <int>, looked <int>, love <int>, melding <int>, memories <int>, overturned <int>,
# past <int>, planting <int>, questions <int>, raw <int>, remember <int>, safe <int>, seldom <int>, shuddered <int>,
# silent <int>, sleep <int>, slip <int>, slowly <int>, smile <int>, summer <int>, surface <int>, tend <int>,
# threw <int>, vision <int>, walks <int>, weary <int>, whisper <int>, world <int>, `10,000` <int>, australian <int>,
# blue <int>, calling <int>, calls <int>, cds <int>, choice <int>, choose <int>, cold <int>, days <int>,
# deserting <int>, euro <int>, feelings <int>, hear <int>, hero <int>, left <int>, maniacs <int>, moment <int>, …library(textrecipes)
# Create recipe for text preprocessing
rec <- recipe(binary_genre ~ text, data = lyrics_data) |>
step_tokenize(text, options = list(strip_punct = T, strip_numeric = T)) |>
step_stopwords(text, language = "en") |>
step_tokenfilter(text, min_times = 20, max_tokens = 1000 ) |>
step_tf(all_predictors())
# "Bake" (check) based on recipe to see text preprocessing
rec |>
prep(train_data) |>
bake(new_data=NULL)# A tibble: 10,445 × 1,001
binary_genre tf_text_2x tf_text_across tf_text_act tf_text_afraid tf_text_ah tf_text_ahead `tf_text_ain't`
<fct> <int> <int> <int> <int> <int> <int> <int>
1 rock 0 0 0 0 0 0 0
2 other 0 0 0 0 0 0 0
3 other 0 0 0 0 0 0 0
4 rock 0 0 0 0 0 0 0
5 other 0 0 0 0 0 0 2
6 rock 0 0 0 0 0 0 2
7 other 0 0 1 0 0 0 1
8 rock 0 1 0 0 0 0 0
9 other 0 0 0 0 0 0 0
10 rock 0 0 0 1 0 0 1
# ℹ 10,435 more rows
# ℹ 993 more variables: tf_text_aint <int>, tf_text_air <int>, tf_text_alive <int>, tf_text_almost <int>,
# tf_text_alone <int>, tf_text_along <int>, tf_text_already <int>, tf_text_alright <int>, tf_text_always <int>,
# tf_text_angel <int>, tf_text_angels <int>, tf_text_another <int>, tf_text_answer <int>, tf_text_anybody <int>,
# tf_text_anymore <int>, tf_text_anyone <int>, tf_text_anything <int>, tf_text_anyway <int>, tf_text_apart <int>,
# tf_text_arms <int>, tf_text_around <int>, tf_text_ask <int>, tf_text_asking <int>, tf_text_ass <int>,
# tf_text_awake <int>, tf_text_away <int>, tf_text_ay <int>, tf_text_b <int>, tf_text_ba <int>, tf_text_babe <int>, …The collection tidymodels contains a variety of packages that facilitates and streamlines machine learning in R
The basic procedure is the following:

# Load specific support library
library(textrecipes)
# Create recipe
rec <- recipe(binary_genre ~ text, data = lyrics_data) |> # <-- predict binary_genre by text
step_tokenize(text, options = list(strip_punct = T, # <-- tokenize, remove punctuation
strip_numeric = T)) |> # <-- remove numbers
step_stopwords(text, language = "en") |> # <-- remove stopwords
step_tokenfilter(text, min_times = 20, max_tokens = 1000) # <-- filter out rare words and use only top 1000 # Load specific support library
library(textrecipes)
# Create recipe
rec <- recipe(binary_genre ~ text, data = lyrics_data) |> # <-- predict binary_genre by text
step_tokenize(text, options = list(strip_punct = T, # <-- tokenize, remove punctuation
strip_numeric = T)) |> # <-- remove numbers
step_stopwords(text, language = "en") |> # <-- remove stopwords
step_tokenfilter(text, min_times = 20, max_tokens = 1000) |> # <-- filter out rare words and use only top 1000
step_tf(all_predictors()) # <-- create document-feature matrix# Load specific support library
library(textrecipes)
# Create recipe
rec <- recipe(binary_genre ~ text, data = lyrics_data) |> # <-- predict binary_genre by text
step_tokenize(text, options = list(strip_punct = T, # <-- tokenize, remove punctuation
strip_numeric = T)) |> # <-- remove numbers
step_stopwords(text, language = "en") |> # <-- remove stopwords
step_tokenfilter(text, min_times = 20, max_tokens = 1000) |> # <-- filter out rare words and use only top 1000
step_tf(all_predictors()) # <-- create document-feature matrix
# Small adaption to the recipe (for SVM and neural networks)
rec_norm <- rec |>
step_normalize(all_predictors()) # A tibble: 6 × 1,001
binary_genre tf_text_2x tf_text_across tf_text_act tf_text_afraid tf_text_ah
<fct> <int> <int> <int> <int> <int>
1 rock 0 0 0 0 0
2 other 0 0 0 0 0
3 other 0 0 0 0 0
4 rock 0 0 0 0 0
5 other 0 0 0 0 0
6 rock 0 0 0 0 0
# ℹ 995 more variables: tf_text_ahead <int>, `tf_text_ain't` <int>,
# tf_text_aint <int>, tf_text_air <int>, tf_text_alive <int>,
# tf_text_almost <int>, tf_text_alone <int>, tf_text_along <int>,
# tf_text_already <int>, tf_text_alright <int>, tf_text_always <int>,
# tf_text_angel <int>, tf_text_angels <int>, tf_text_another <int>,
# tf_text_answer <int>, tf_text_anybody <int>, tf_text_anymore <int>,
# tf_text_anyone <int>, tf_text_anything <int>, tf_text_anyway <int>, …There are many different “algorithms” or classifiers that we can use:
Most of these algorithms have certain hyperparameters that need to be set
Unfortunately, there is no good theoretical basis for selecting an algorithm or hyperparameters
Using the Bayes Theorem for Classification
Goes back to the Bayes’ Theorem published in 1763!
Computes the prior probability ( P ) for every category ( c = outcome variable ) based on the training data set
Computes the probability of every feature ( x ) to be a characteristic of the class ( c ); i.e., the relative frequency of the feature in category
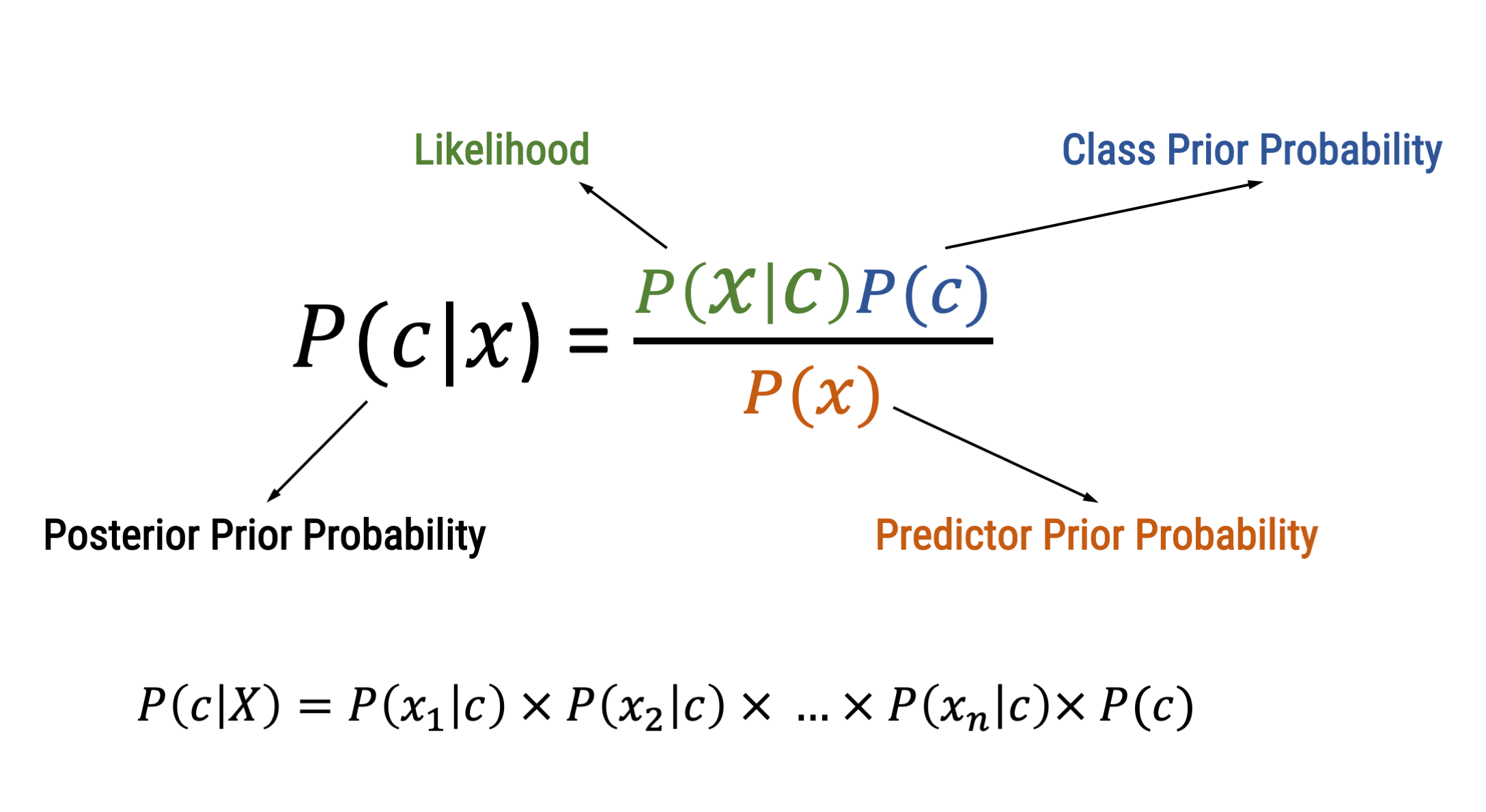
For every probability of a category in light of certain features ( P(c|X) ), all feature probabilities ( x ) are multiplied
The algorithm hence chooses the class that has highest weighted sum of inputs
\(P(rock|death) = \frac{P(death|rock) * P(rock)}{P(death)} = \frac{.15 * .54}{.05} = .162\)
Lantz, 2013
# Create workflow
nb_workflow <- workflow() |> # We initiate a workflow
add_recipe(rec) |> # We add our text preprocessing recipe to the workflow
add_model(naive_Bayes(mode = "classification", # We choose Naive Bayes for classification
engine = "naiveBayes")) # Engine = R package to be used
# Fitting the naive bayes model
m_nb <- fit(nb_workflow, data = training(split)) # Fitting the modelUsing the function conf_mat on the actual and predicted genre columns, we can now inspect the confusion matrix
We already see that there are many “false-positives” (1890!), but less false negatives.
tidymodels, we have to define a set of measures that we want to compute based on the predictions in the test set.Overall accuracy is 69%, which is better than chance, but not very good.
Precision is also low because of a lot of false positives (65.2%)
Yet, recall is quite high as only few rock songs were classified as another genre (92.9%)
Why not use a simple statistical model for binary classification
As mentioned earlier, a linear regression can be described with the following formula:
\(Y_i = b_0 + b_1 x_i + \epsilon_i\)
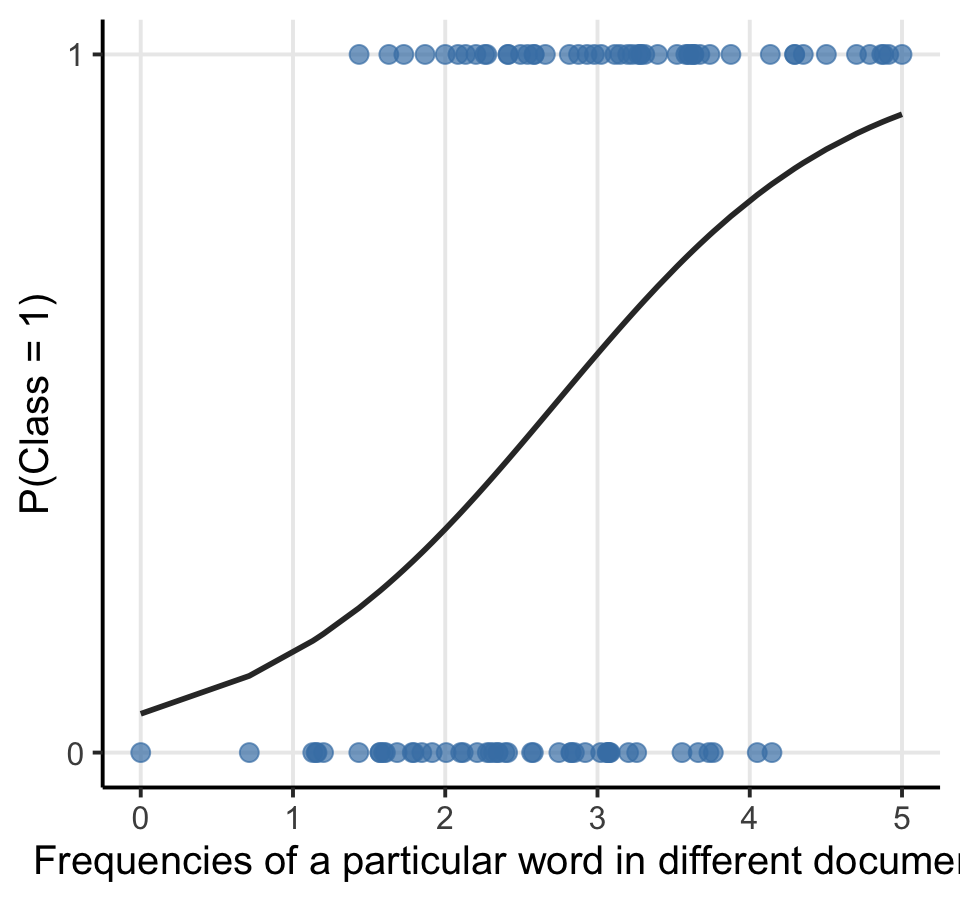
When we classify text, the dependent variable (the outcome class: \(Y_i\)) is not metric, but has only two values (1 = “is class”, 0 = “is not class”).
We thus need to estimate the probability of \(Y = 1\) by using the so-called sigmoid function:
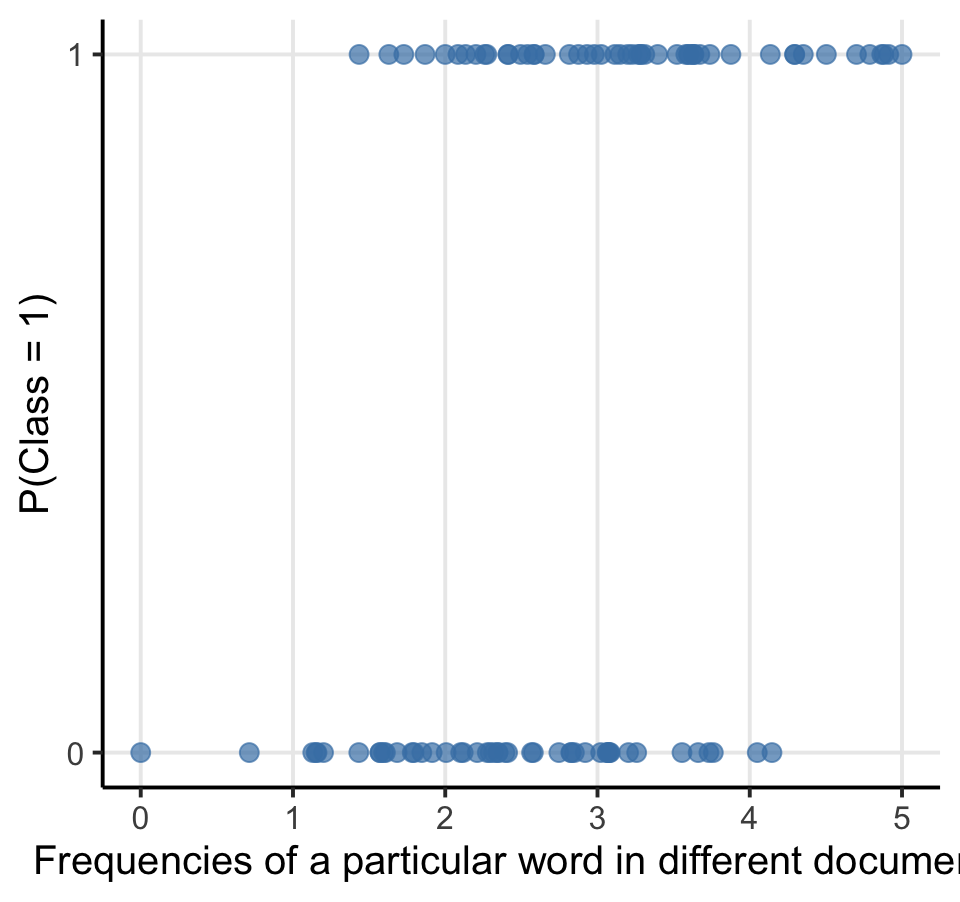
In both classic statistics as well as machine learning, this is know as logistic regression
In machine learning, we see it as an algorithm that accomplishes binary classification tasks by predicting the probability of an outcome, event, or observation
To train a classifier during text classification tasks, we simply fit a logistic regression model with all text features (e.g., the frequencies of words per document) as input (predictors) and provide the outcome class as output (dependent variable)
In contrast to statistical models that use logistic regression, the machine learning model contains thus only much more variables!
Lantz, 2013
# Additional package needed
library(discrim)
# Creating a workflow
lr_workflow <- workflow() |> # Initate the workflow
add_recipe(rec) |> # Add recipe
add_model(logistic_reg(mixture = 0, penalty = 0.1, # Choose logistic regression
engine = "glm")) # Standard engine
# Fitting the logistic regression model
m_logistic <- fit(lr_workflow, data = training(split)) # Fit modelOverall accuracy of the Logistic Regression classifier is 74.7%, which is better than the Naive Bayes!
Precision is also ok due to less false positives (73.8%)
Yet, recall is slightly lower, but still good (83.3%)
m_logistic |>
extract_fit_parsnip() |>
vip::vi() |>
group_by(Sign) |>
mutate(Sign = recode(Sign,
POS = "negative",
NEG = "positive")) |>
top_n(20, wt = abs(Importance)) |>
ungroup() |>
mutate(
Importance = abs(Importance),
Variable = str_remove(Variable, "tf_text_"),
Variable = fct_reorder(Variable, Importance)
) |>
ggplot(aes(x = Importance,
y = Variable,
fill = Sign)) +
geom_col(show.legend = FALSE) +
facet_wrap(~Sign, scales = "free_y") +
labs(y = NULL)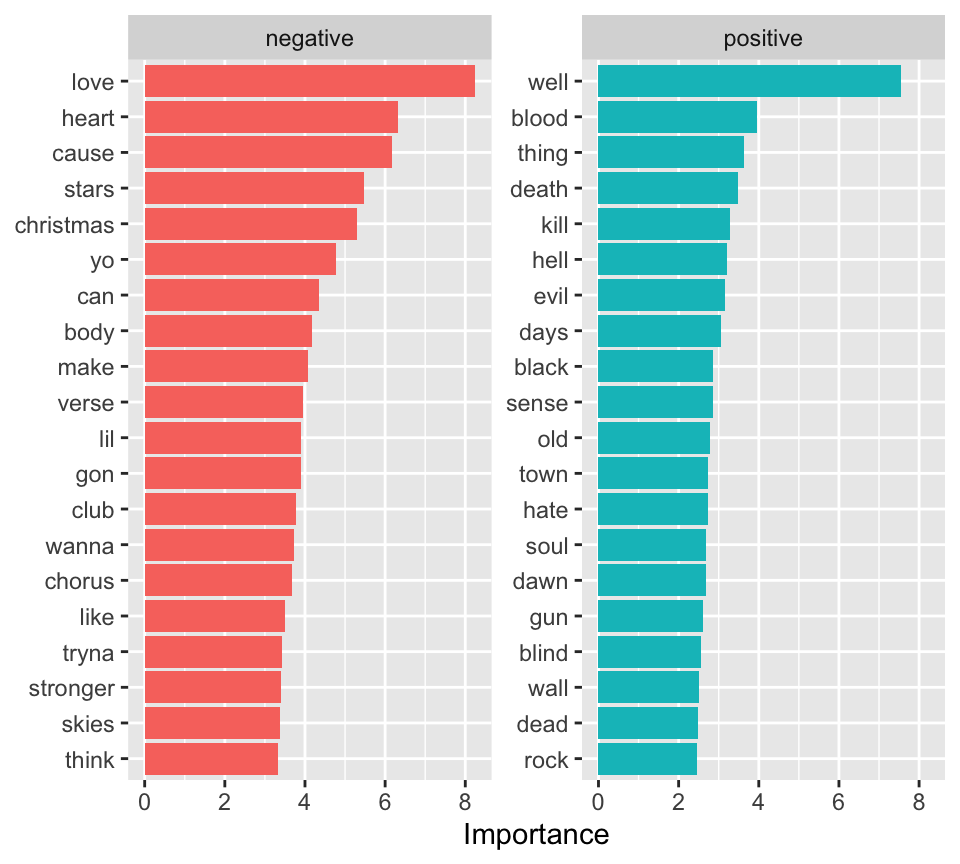
A versatile black box method
Very often used machine learning method, due to its high performance in a variety of tasks
A support vector machine (SVM) can be imagined as a “surface” that creates the greatest separation between two groups in a multidimensional space representing classes and their feature values
Tries to find decision boundary between points that maximizes margin between classes while minimizing errors
More formally, a support-vector machine constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space (wait what?)
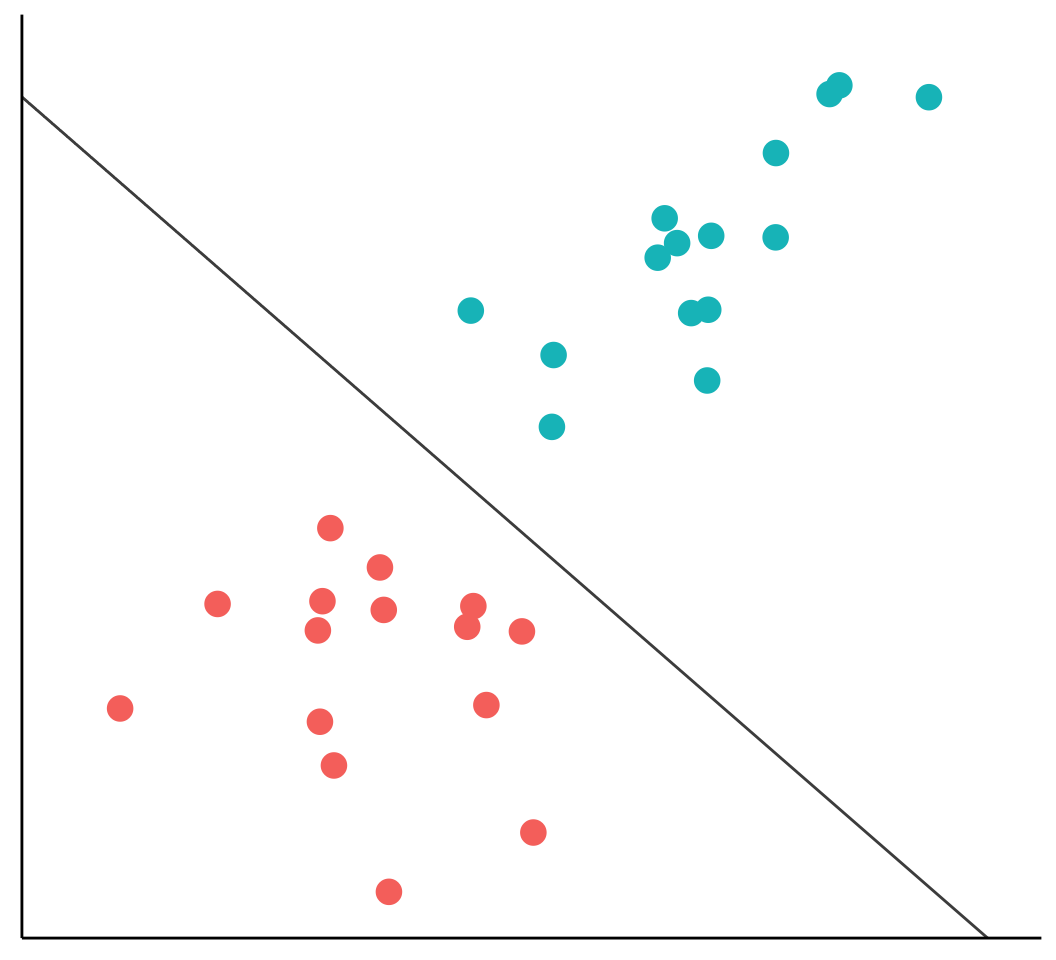
The following figure depicts two groups of data that can be plotted in two dimensions (here, I show only two dimensions because it is difficult to imagine or illustrate space in greater than two dimensions)
Because the groups are perfectly separatable by a straight line, they are said to be linearly separable (but hyperplanes don’t have to be linear)
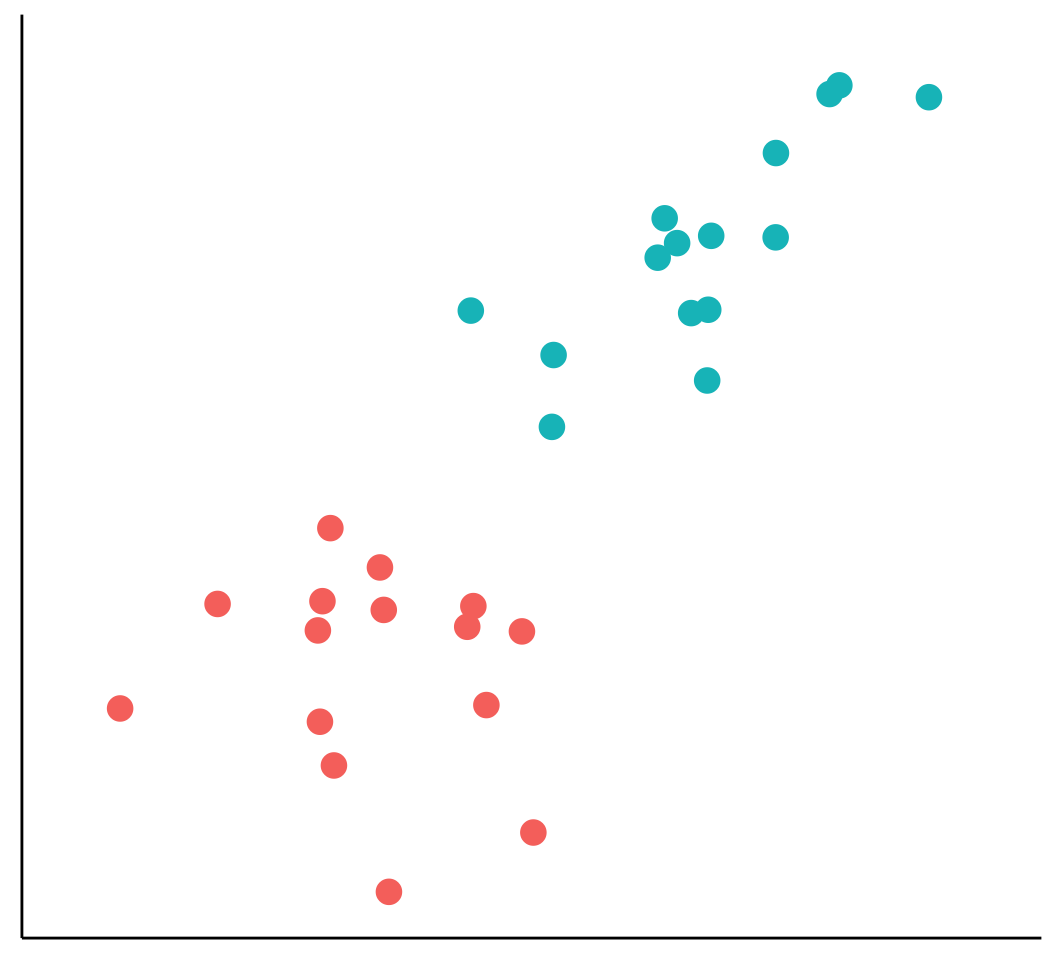
The following figure depicts two groups of data that can be plotted in two dimensions (here, I show only two dimensions because it is difficult to imagine or illustrate space in greater than two dimensions)
Because the groups are perfectly separatable by a straight line, they are said to be linearly separable (but hyperplanes don’t have to be linear)
The task of the SVM algorithm is to identify a line that separates the two classes, but there os always more than one choice
Therefore, the algorithm searches for the maximum margin hyperplane (MMH) that creates the greatest separation between the two classes, although any of the three lines separates the classes, the line that leads to the greatest separation will generalize best to new data
The support vectors are the points from each class that are closest to the MMH (each class must have at least on support vector)
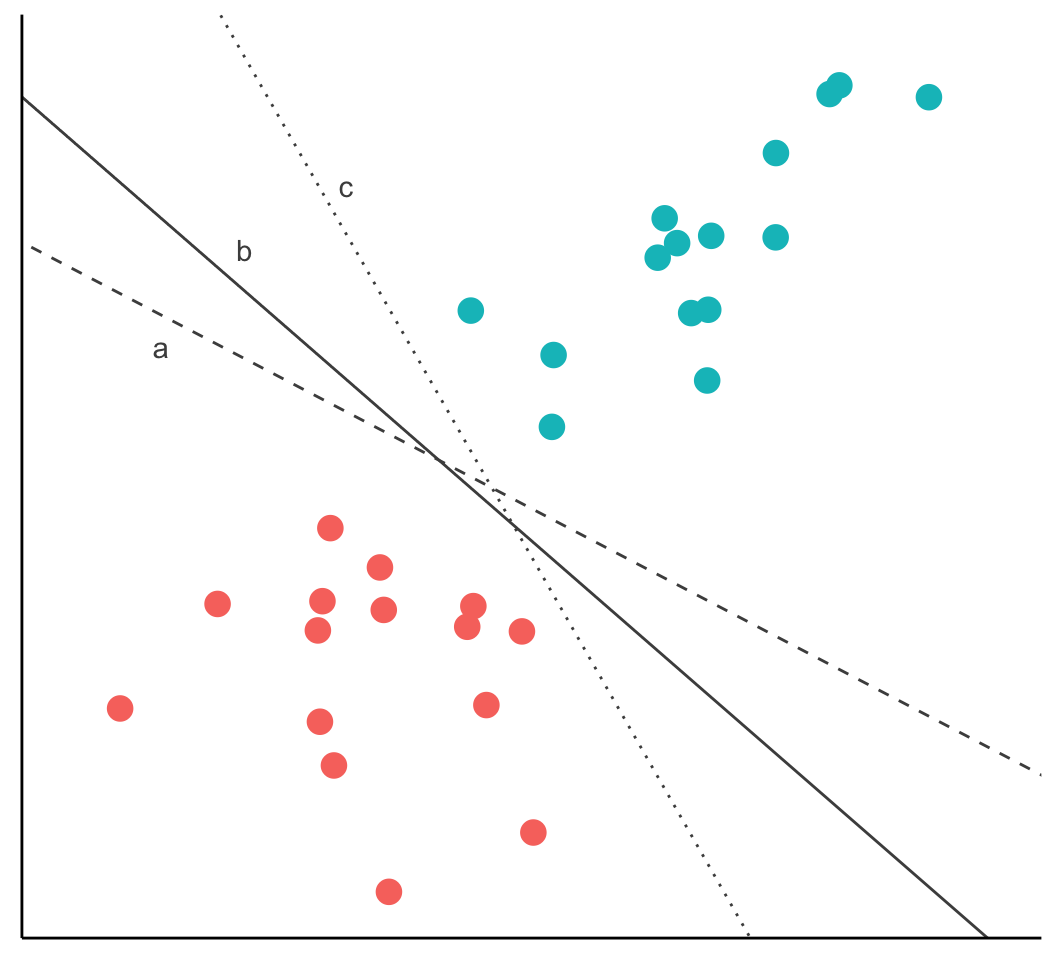
The task of the SVM algorithm is to identify a line that separates the two classes, but there os always more than one choice
Therefore, the algorithm searches for the maximum margin hyperplane (MMH) that creates the greatest separation between the two classes, although any of the three lines separates the classes, the line that leads to the greatest separation will generalize best to new data
The support vectors are the points from each class that are closest to the MMH (each class must have at least on support vector)
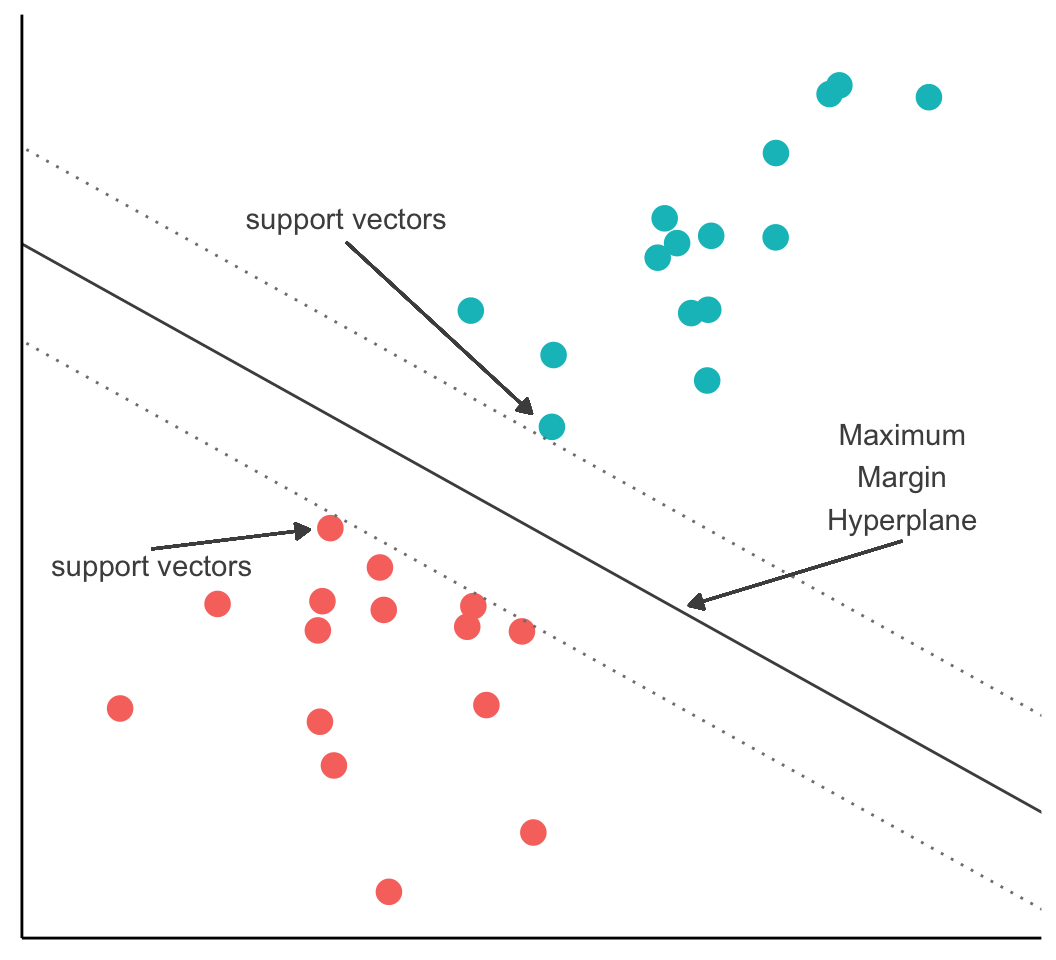
Lantz, 2013
Overall performance is very similar to logistic regression
Can probably be improved with fine-tuning of hyper-parameters
The human brain abstracted to a numerical model
An artificial neural network (ANN) models the relationship between a set of input signals and an output signal using a model derived from our understanding of the human brain
Like a brain uses a network of interconnected cells called “neurons” (a) to provide fast learning capabilities, ANN uses a network of artificial neurons (b) to solves learning tasks
Source: Arthur Arnx/Medium
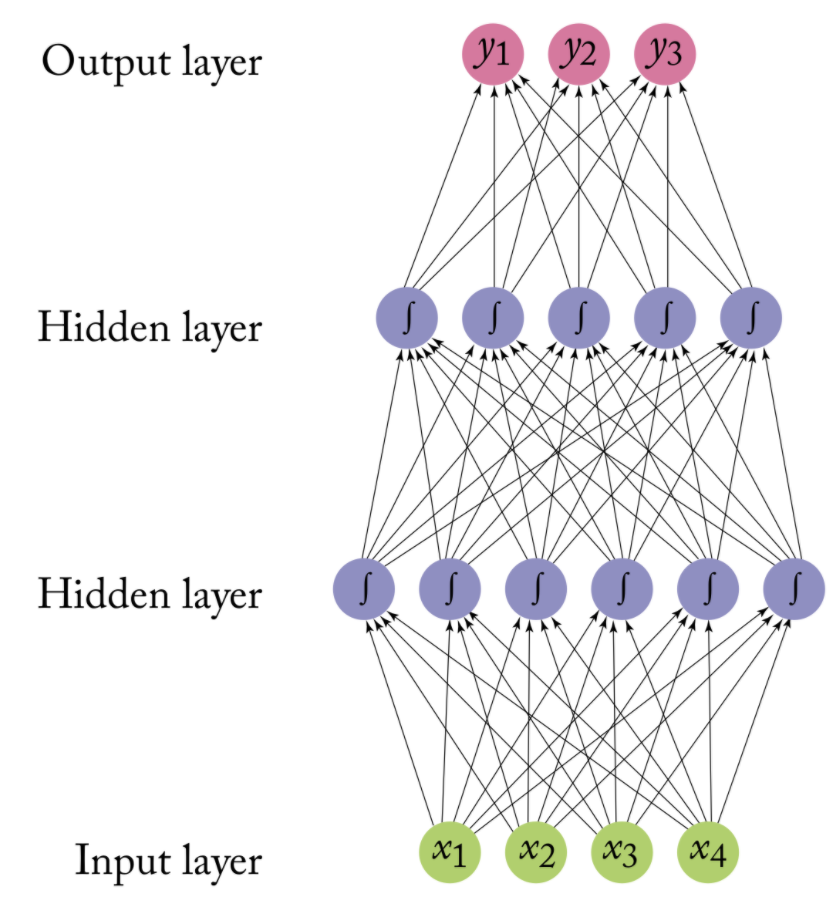
The operation of an ANN is straightforward:
In the simplest form, neurons on are stacked on top of one another and a neuron of colum n can only be connected to inputs from column n-1 and provide outputs to neurons in column n+1
First, a neuron adds up the value of every neurons from the previous column it is connected to (here x1, x2, and x3)
This value is multiplied, before being added, by another variable called “weight” (w1, w2, w3): the strength of connection between two neurons
A bias value may be added (e.g., to regularize the network)
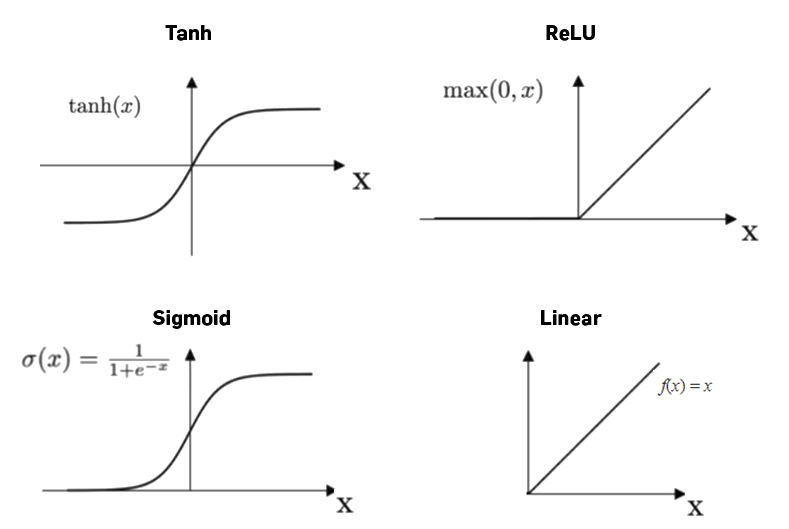
After all those summations, the neuron finally applies a function called activation function to the obtained value
Source: Arthur Arnx/Medium
The activation function serves to turn the total value calculated to a number between 0 and 1
A threshold then defines at what value the function should “fire” the output to the next neuron (of course this can be probabilistic)
We can choose from different activation functions; which works best is sometimes hard to tell
 In a first try, the ANN randomly sets weights and thus can’t get the right output (except with luck)
In a first try, the ANN randomly sets weights and thus can’t get the right output (except with luck)
If the (random) choice was a good one, actual parameters are kept and the next input is given. If the obtained output doesn’t match the desired output, the weights are changed.
To determine which weight is better to modify, a ANN uses backpropagation, which consists of “going back” on the neural network and inspect every connection to check how the output would behave according to a change on the weight
The learning rate thereby determines the speed a neural network will learn, i.e., how it will modify a weight (e.g., little by little or by bigger steps).
Learning rate and number of learning cycles (epochs) have to be set manually upfront!

A simple model with just inputs and outputs is called a perceptron
Despite its usefulness for many tasks, it cannot combine features
But we can add “hidden” layers (latent variables), creating a multilayer perceptron, which is able to process more complex inputs
Backpropagation is thus the way a neural network adjusts the weights of its connections (-> Can take a long time to find the right solutions)
Universal approximator: Neural Networks with single hidden layer can represent every continuous function!
Lantz, 2013
# For replication purposes
set.seed(42)
# Specify multilayer perceptron
nnet_spec <-
mlp(epochs = 400, # <- times that algorithm will work through train set
hidden_units = c(6), # <- nodes in hidden units
penalty = 0.01, # <- regularization
learn_rate = 0.2) |> # <- shrinkage
set_engine("brulee") |> # <-- engine = R package
set_mode("classification")# For replication purposes
set.seed(42)
# Specify multilayer perceptron
nnet_spec <-
mlp(epochs = 400, # <- times that algorithm will work through train set
hidden_units = c(6), # <- nodes in hidden units
penalty = 0.01, # <- regularization
learn_rate = 0.2) |> # <- shrinkage
set_engine("brulee") |> # <-- engine = R package
set_mode("classification")# For replication purposes
set.seed(42)
# Specify multilayer perceptron
nnet_spec <-
mlp(epochs = 400, # <- times that algorithm will work through train set
hidden_units = c(6), # <- nodes in hidden units
penalty = 0.01, # <- regularization
learn_rate = 0.2) |> # <- shrinkage
set_engine("brulee") |> # <-- engine = R package
set_mode("classification")# For replication purposes
set.seed(42)
# Specify multilayer perceptron
nnet_spec <-
mlp(epochs = 400, # <- times that algorithm will work through train set
hidden_units = c(6), # <- nodes in hidden units
penalty = 0.01, # <- regularization
learn_rate = 0.2) |> # <- shrinkage
set_engine("brulee") |> # <-- engine = R package
set_mode("classification")
# Create workflow
ann_workflow <- workflow() |>
add_recipe(rec_norm) |> # Use updated recipe with normalization
add_model(nnet_spec)# For replication purposes
set.seed(42)
# Specify multilayer perceptron
nnet_spec <-
mlp(epochs = 400, # <- times that algorithm will work through train set
hidden_units = c(6), # <- nodes in hidden units
penalty = 0.01, # <- regularization
learn_rate = 0.2) |> # <- shrinkage
set_engine("brulee") |> # <-- engine = R package
set_mode("classification")
# Create workflow
ann_workflow <- workflow() |>
add_recipe(rec_norm) |> # Use updated recipe with normalization
add_model(nnet_spec)
# Fit model
m_ann <- fit(ann_workflow, train_data)Highest accuracy of all four algorithms (74.9%)
Most balanced performance scores
Yet, performance overall similar to logistic regression and SVM
You may have noticed that I always set some hyperparameter in all of the models
There is no clear rule of how to set these parameters and their influence on performance is often unknown
Using trail and error, we simply compare many different model specifications to find optimal hyperparameters
Very good examples are the hyperparameters of support vector machines: it is hard to know how soft our margins should be and we may also be unsure about the right kernel , or in the case of a polynomial kernel, how many degrees we want to consider
Similarly, we have to simply try out whether a neural network needs more than one hidden layer or how many nodes make sense, what learning rate works best, etc.
Good machine learning practice is to conduct a so-called grid-search, i.e. systematically run combinations of different specifications (but computationally expensive!!!)
Hvitfeld & Silge (2021)
# Create a model function for tuning a multilayer perceptrion neural network
mlp_spec <- mlp(hidden_units = tune(),
penalty = tune(),
epochs = tune()) |>
set_engine("brulee", trace = 0) |>
set_mode("classification")
# Estract "dials" for parameter tuning
mlp_param <- extract_parameter_set_dials(mlp_spec)
# Simple combinatorial design
mlp_param |> grid_regular(levels = c(hidden_units = 2, penalty = 2, epochs = 2)) # Create a model function for tuning a multilayer perceptrion neural network
mlp_spec <- mlp(hidden_units = tune(),
penalty = tune(),
epochs = tune()) |>
set_engine("brulee", trace = 0) |>
set_mode("classification")
# Estract "dials" for parameter tuning
mlp_param <- extract_parameter_set_dials(mlp_spec)
# Random design with 1000 combinations
mlp_param |> grid_random(size = 1000) |> summary()We can plot the random combinations to get an idea what they will cover
Bear in mind, such a grid search would be quite computationally intensive as 50 neural networks would need to be fitted!
set.seed(42)
# Create new workflow
mlp_wflow <- workflow() |>
add_recipe(rec_norm) |>
add_model(mlp_spec)
# Adjust parameter extremes
mlp_param <- mlp_wflow |>
extract_parameter_set_dials() |>
update(epochs = epochs(c(200, 600)),
hidden_units = hidden_units(c(1, 9)),
penalty = penalty(c(-10, -1)))
# Set metric of interest
acc <- metric_set(accuracy)
# Define resampling strategy
twofold <- vfold_cv(lyrics_data, v = 2)
# Run the tuning process
mlp_reg_tune <- mlp_wflow |>
tune_grid(
resamples = twofold,
grid = mlp_param |>
grid_regular(levels = c(hidden_units = 4, penalty = 4, epochs = 3)),
metrics = acc
)The result of this tuning grid search is a table that shows the best combinations of parameters in descending order
We can see here that 9 nodes in one hidden layer, a penalty of 0.0001 and 600 epochs lead to the best accuracy, but it is actually worse than our original model with 6 nodes and a penalty of 0.001 and 400 epochs
# Get best fit
best_fit <- show_best(mlp_reg_tune, n = 48) |>
select(-.estimator, -.config, -.metric) |>
rename(accuracy = mean)
best_fit# A tibble: 48 × 6
hidden_units penalty epochs accuracy n std_err
<int> <dbl> <int> <dbl> <int> <dbl>
1 9 0.0001 600 0.746 2 0.00125
2 3 0.1 600 0.745 2 0.00849
3 9 0.1 600 0.745 2 0.00918
4 6 0.0001 600 0.743 2 0.00429
5 9 0.0000000001 600 0.742 2 0.00447
6 6 0.0000000001 600 0.742 2 0.00211
7 6 0.0000001 600 0.741 2 0.00257
8 9 0.0000001 600 0.740 2 0.000674
9 3 0.0000001 600 0.740 2 0.000360
10 1 0.1 600 0.739 2 0.00182
# ℹ 38 more rowspredict function and supply the new songs. This code could of course also be used in a software that detects genre from song lyricScharkow ran a simple simulation study in which he systematically varied text preprocessing
The classifier was always Naive Bayes, below we see the average difference in performance
Task difficulty
Amount of training data
Choice of features (n-grams, lemmata, etc)
Text preprocessing (e.g., exclude or include stopwords?)
Representation of text (tf, tf-idf, word-embedding)
Tuning of algorithm (what we did in the grid search)
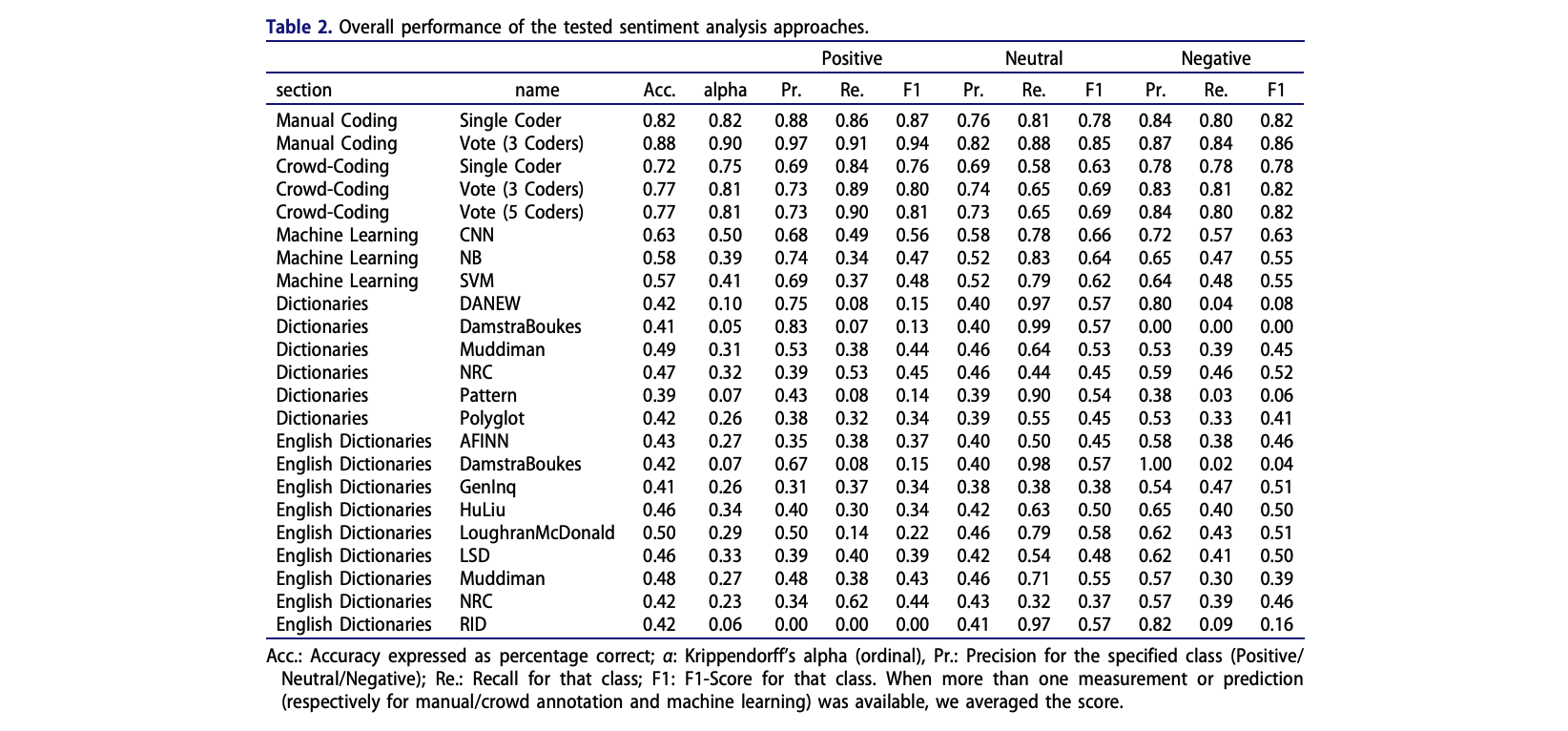
Van Atteveldt et al. (2021) re-analysised data reported in Boukes et al. (2020) to understand the validity of different text classification approaches for sentiment analysis
The data included news from a total of ten newspapers and five websites published between February 1 and July 7, 2015:
How Machine Learning is used in Communication Science
Su et al. (2018) examined the extent and patterns of incivility in the comment sections of 42 US news outlets’ Facebook pages in 2015–2016
News source outlets included
Implemented a combination of manual coding and supervised machine learning to code:
de León et al. (2021) explored how elections transform news sharing behaviour on Facebook
They investigated changes in news coverage and news sharing behaviour on Facebook
Employed a novel data set of news articles (N = 83,054) in Mexico
First coded 2,000 articles manually into topics (Politics, Crime and Disasters, Culture and Entertainment, Economic and Business, Sports, and Other), then used support vector machines to classify the rest

During periods of heightened political activity, both the publication and dissemination of political news increases
The gap between the news choices of journalists and consumers narrows, and increased political news sharing leading to a decrease in the sharing of other news.
Next week, we reach the present!
Machine learning in the social sciences generally used to solve an engineering problem
Output of Machine Learning is input for “actual” statistical model (e.g., we classify text, but run an analysis of variance with the output)
Ethical concerns
Is it okay to use a model we can’t possibly understand (e.g., SVM, neural networks)?
If they lead to false positives or false negatives, which in turn discriminate someone or lead to bias, it is difficult to find the source and denote responsibility
We always need to validate model on unseen and representative test data!
Think before you run models or you will waste a lot of computational resources
Classic machine learning is a useful tool for generalizing from a sample
It is very useful to reduce the amount of manual coding needed
That said, the field has moved on and innovations are fast-paced these days:
van Atteveldt, W., van der Velden, M. A. C. G., & Boukes, M.. (2021). The Validity of Sentiment Analysis: Comparing Manual Annotation, Crowd-Coding, Dictionary Approaches, and Machine Learning Algorithms. Communication Methods and Measures, (15)2, 121-140, https://doi.org/10.1080/19312458.2020.1869198
Su, L. Y.-F., Xenos, M. A., Rose, K. M., Wirz, C., Scheufele, D. A., & Brossard, D. (2018). Uncivil and personal? Comparing patterns of incivility in comments on the Facebook pages of news outlets. New Media & Society, 20(10), 3678–3699. https://doi.org/10.1177/1461444818757205
(available on Canvas)
Boumans, J. W., & Trilling, D. (2016). Taking stock of the toolkit: An overview of relevant automated content analysis approaches and techniques for digital journalism scholars. Digital journalism, 4(1), 8-23.
de León, E., Vermeer, S. & Trilling, D. (2023). Electoral news sharing: a study of changes in news coverage and Facebook sharing behaviour during the 2018 Mexican elections. Information, Communication & Society, 26(6), 1193-1209. https://doi.org/10.1080/1369118X.2021.1994629
Hvitfeld, E. & Silge, J. (2021). Supervised Machine Learning for Text Analysis in R. CRC Press. https://smltar.com/
Lantz, B. (2013). Machine learning in R. Packt Publishing Ltd.
Scharkow, M. (2013). Thematic content analysis using supervised machine learning: An empirical evaluation using german online news. Quality & Quantity, 47(2), 761–773. https://doi.org/10.1007/s11135-011-9545-7
Su, L. Y.-F., Xenos, M. A., Rose, K. M., Wirz, C., Scheufele, D. A., & Brossard, D. (2018). Uncivil and personal? Comparing patterns of incivility in comments on the Facebook pages of news outlets. New Media & Society, 20(10), 3678–3699. https://doi.org/10.1177/1461444818757205
van Atteveldt, W., van der Velden, M. A. C. G., & Boukes, M.. (2021). The Validity of Sentiment Analysis: Comparing Manual Annotation, Crowd-Coding, Dictionary Approaches, and Machine Learning Algorithms. Communication Methods and Measures, (15)2, 121-140, https://doi.org/10.1080/19312458.2020.1869198
Van Atteveldt and colleagues (2020) tested the validity of various automated text analysis approaches. What was their main result?
A. English dictionaries performed better than Dutch dictionaries in classifying the sentiment of Dutch news paper headlines.
B. Dictionary approaches were as good as machine learning approaches in classifying the sentiment of Dutch news paper headlines.
C. Of all automated approaches, supervised machine learning approaches performed the best in classifying the sentiment of Dutch news paper headlines.
D. Manual coding and supervised machine learning approaches performed similarly well in classifying the sentiment of Dutch news paper headlines.
Van Atteveldt and colleagues (2020) tested the validity of various automated text analysis approaches. What was their main result?
A. English dictionaries performed better than Dutch dictionaries in classifying the sentiment of Dutch news paper headlines.
B. Dictionary approaches were as good as machine learning approaches in classifying the sentiment of Dutch news paper headlines.
C. Of all automated approaches, supervised machine learning approaches performed the best in classifying the sentiment of Dutch news paper headlines.
D. Manual coding and supervised machine learning approaches performed similarly well in classifying the sentiment of Dutch news paper headlines.
Describe the typical process used in supervised text classification.
Any supervised machine learning procedure to analyze text usually contains at least 4 steps:
One has to manually code a small set of documents for whatever variable(s) you care about (e.g., topics, sentiment, source,…).
One has to train a machine learning model on the hand-coded /gold-standard data, using the variable as the outcome of interest and the text features of the documents as the predictors.
One has to evaluate the effectiveness of the machine learning model via cross-validation. This means one has to test the model test on new (held-out) data.
Once one has trained a model with sufficient predictive accuracy, precision and recall, one can apply the model to more documents that have never been hand-coded or use it for the purpose it was designed for (e.g., a spam filter detection software)

Computational Analysis of Digital Communication