Text Classification Using Classic Machine Learning

Week 3: Neural Networks and Word-Embeddings

Dr. Philipp K. Masur

So what are we actually talking about?

• Machine learning is the study of computer algorithms that can improve automatically through experience and by the use of data

• Due to the “black box” nature of the algorithm’s operations, it is often seen as a form of artificial intelligence

Source: qlik

Some success stories

Successful machine learning in practical contexts:

• Identification of spam messages in mails
• Segmentation of customers for targeted advertising
• Weather forecasts and long-term climate changes
• Reduction of fraudulent credit card transactions
• Prediction of election outcomes
• Auto-piloting and self-driving cars
• Face recognition
• Discovery of genetic sequences linked to diseases
• ….

Content of this lecture

1. What is Machine Learning?

   1.1. Concepts and Principles

   1.2. The General Machine Learning Pipeline

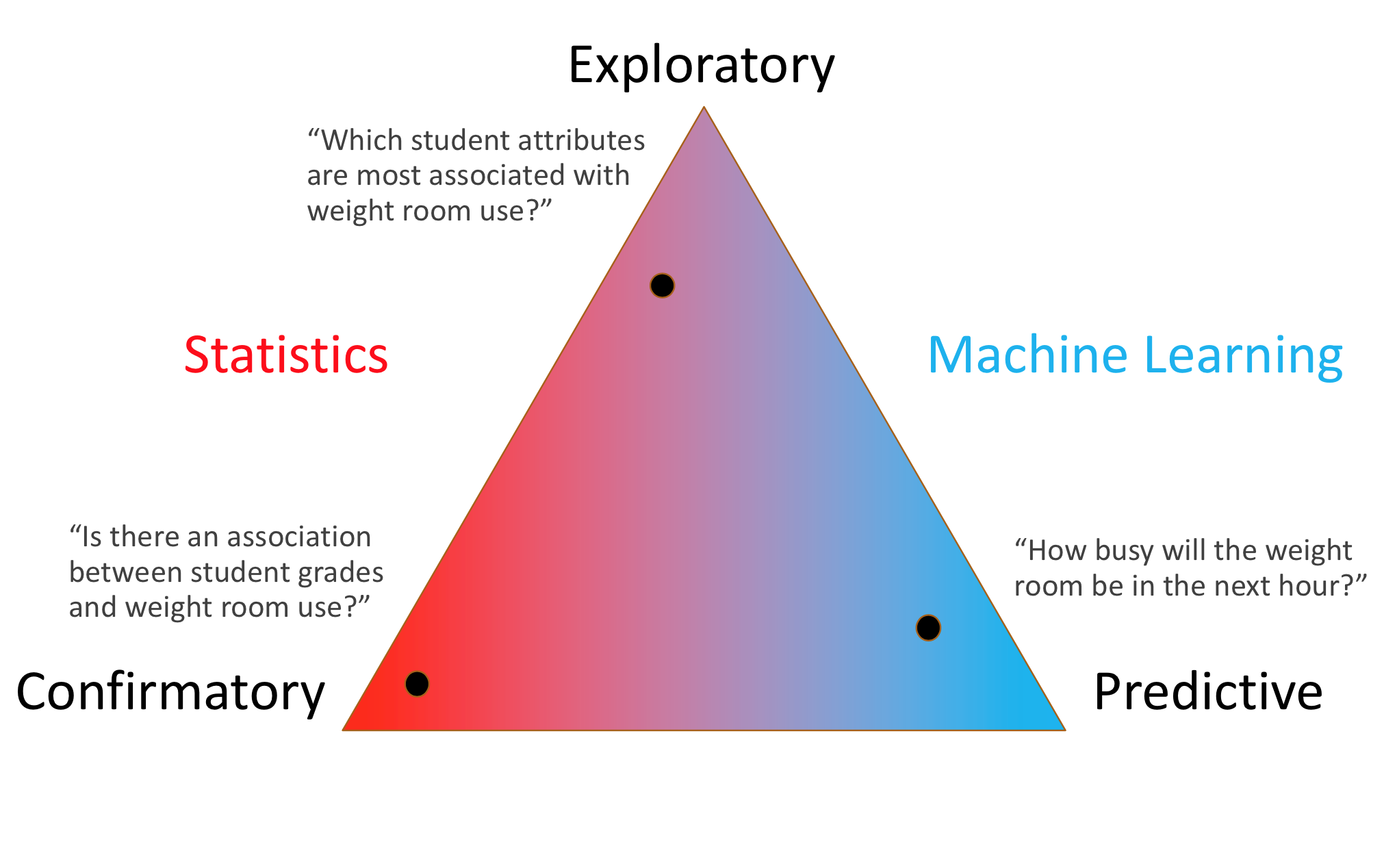
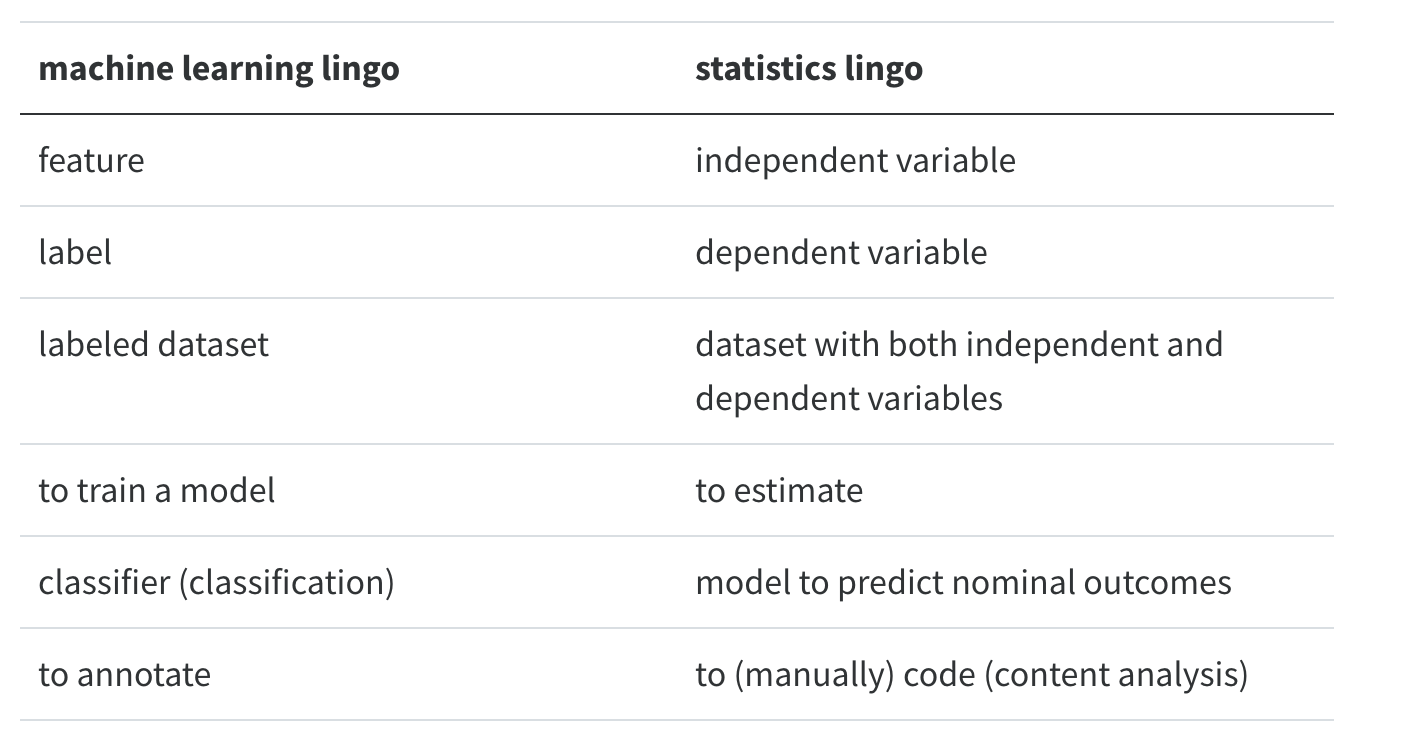
   1.3. Difference between Statistics and Machine Learning

   1.4. Over- vs. underfitting

   1.5. Training vs. Testing

2. Text Classification with Artificial Neural Networks

   2.1. Overview of classic ML algorithms

   2.2. General Idea behind Neural Networks

   2.3. How A Neural Network Works

   2.4. How A Neural Network Learns

   2.5. Example using Actual Data

3. More Complex Text Representations: Word-Embeddings

   3.1. Basic Idea behind Vector-Representations

   3.2. Similarity of Words and Texts

   3.3. Using Pre-trained Word-Embeddings: GloVe

4. Text Classification with Word-Embeddings

   4.1. Text Classification Pipeline with Word-Embeddings

   4.2. Example with Actual Data

   4.4. Fine-Tuning and Grid Search

5. Examples from the Literature

   4.1. Incivility on Facebook (Su et al., 2018)

   4.2. Electoral News Sharing (de León et al., 2021)

6. Summary and Conclusion

What is machine learning?

Understanding Supervised Machine Learning Approaches

Deductive vs. inductive approaches

• In the previous lecture, we talked about deductive approaches (e.g., dictionary approaches)

• These are deterministic and are based on a priori text theory
  (e.g., happy → positive, hate → negative)

• Yet, natural language is often ambiguous and a probabilistic coding may be better

• Dictionary-based or generally rule-based approaches are not very similar to manual coding; a human being assesses much more than just a list of words

• Inductive approaches promise to combine the scalability of automatic coding with the validity of manual coding

Supervised vs. Unsupervised Approaches

Example of supervised text classification

General text classification pipeline

Supervised Text Classification Pipeline

Statistical Modeling vs. Supervised Machine learning

• Machine learning, many people joke, is nothing but a fancy name for statistics.

• There is some truth to this: the term “logistic regression” will sound familiar to both statisticians and machine learning practitioners.

• Still, there are some differences between traditional statistical approaches and the machine learning approach, even if some of the same mathematical tools are used.

Source: Demetri Pananos/stackoverflow

Statistical Modeling

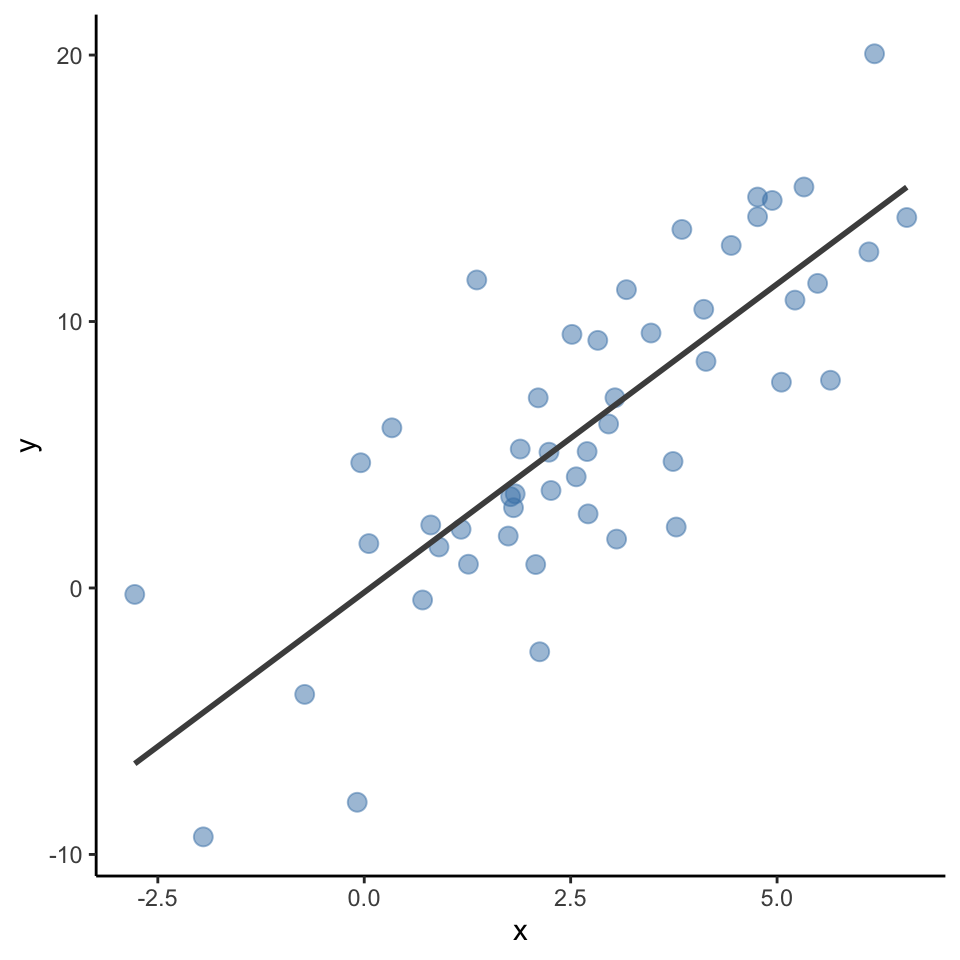
• Is about understanding the relationship between one (or several) predictor(s) and an outcome variable

• Learn \(f\) so you can predict \(y\) from \(x\):

\(y = f(x)\)

• In a linear regression model, we try to findt he best fitting “line” that best predicts \(y\) based on \(x\):

\(y = -0.16 + 2.31 * x + \epsilon\)

• We then say: when x increases by 1 unit,y increases by 2.31 units.

Machine Learning

• Machine learning less about not understanding, but about maximizing prediction

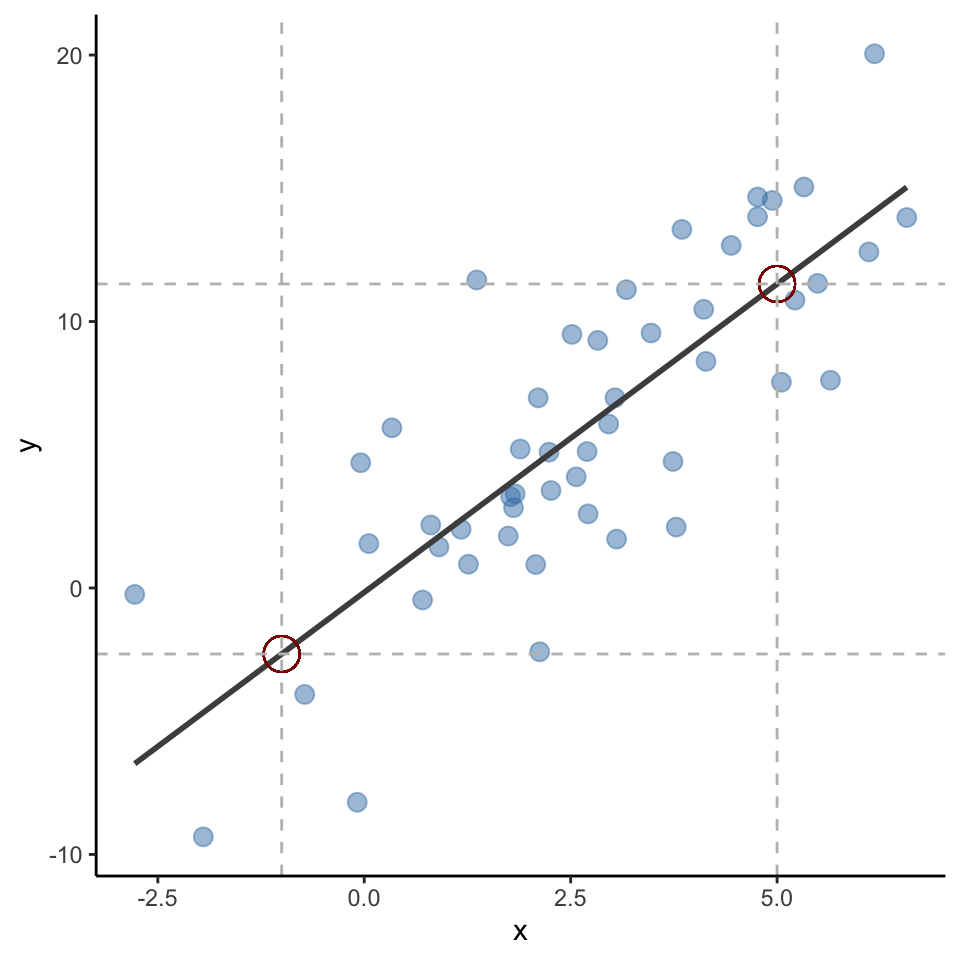
• A statistical model can be used to predict most likely \(y\) values based on new \(x\) data.

• For example, despite not being in the data, \(x = -1\) should be \(y = -2.47\); \(x = 5\) should be \(y = 11.41\) based on the fitted line

• In other words, machine learning doesn’t focus on explanation, but emphasizes prediction

Differences in language

Source: van Atteveldt et al., 2021

Differences in Goals

• Goal of statistical modeling: explaining/understanding

  • Serves to make inferences about a population (“Does \(X\) relate to \(Y\)?”)
  • Doesn’t use too many variables to avoid the difficulty of interpreting too many parameters
  • Requires interpretable parameters

• Goal of machine learning: best possible prediction

  • make generalizable predictions (“How to best predict \(Y\)?”)
  • We do not care about the actual values of the coefficients, we just need them for our prediction
  • We will often have so many of them that we do not even bother to report them

Note: Machine learning models often have 1000’s of colinear independent variables and can have many latent variables!

Over- vs. underfit

• Problem in Machine Learning: Sufficiently complex algorithms can predict all training data perfectly

• But such an algorithm does not generalize to new data

• Essentially, we want the model to have a good fit to the data, but we also want it to not optimize on things that are specific to the training data set

• Let’s try exemplify over vs. underfit with some simulated data!

Examplifying over- and underfit

Linear fit (underfit)

Overfit

Good fit

Preventing overfitting

• Regularization during fitting process

  • ‘Punish’ complexity
  • Constrain flexibility
  • Removing noise

• Out-of-sample validation

  • To see whether a model generalizes to new data, simply test it on new data
  • This validation set clearly detects overfitting

Solution: Training and Testing

• As models (almost) always overfit, performance on only training data is not a good indicator of the real quality of the classifier

• The standard solution is to split the labeled data into a training and test data sets: We train the algorithm on one part and then evaluate its performance on the held-out part

• In more elaborate scenarios, we distinguish in training, validation, and testing sets

Integrating testing in the pipeline

Testing = Validation

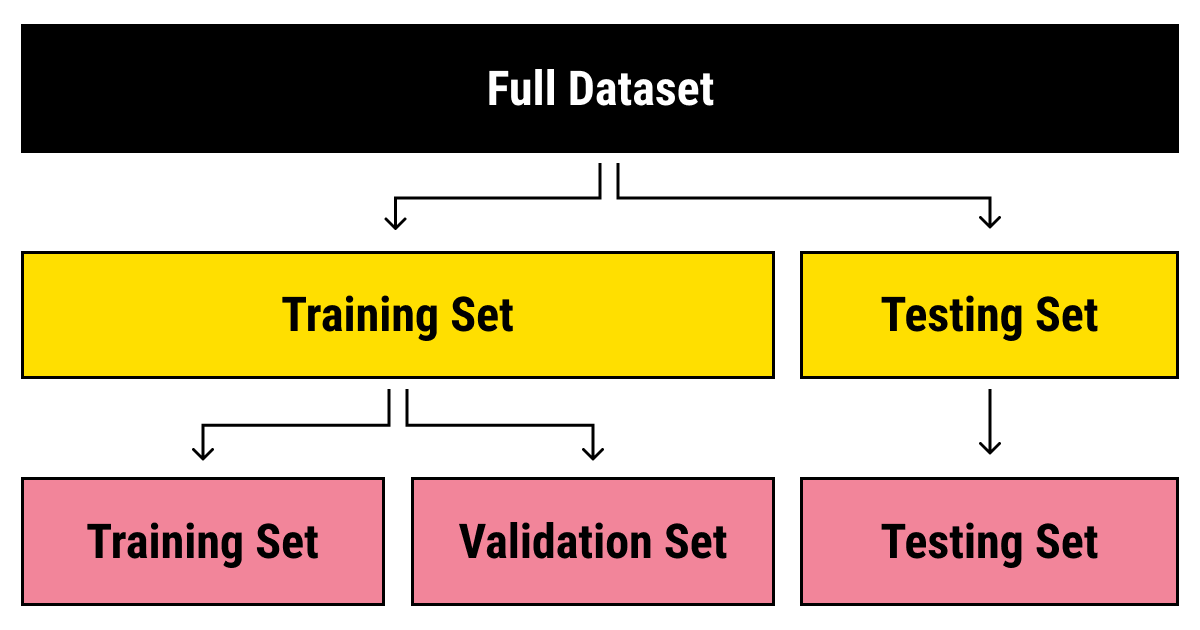
• Remember how we validated dictionary approaches?

  • We manually coded a small set of the text
  • Compared this gold standard to the dictionary result

• In supervised text classification, the procedure is similar:

  • We use the classifier, trained on the training data, to predict the outcome in the test data
  • Because the test data is only a subset of our labeled data, it also contains the true outcome
  • We compare the predicted with the actual outcome and compute the performance scores (Accuracy, Precision,…)

Text Classification with Artificial Neural Networks

Translating the Architecture of the Brain into Algorithmic Processing

Overview of different ML algorithms

→ In the following, we will focus primarily on neural networks as the most advanced algorithm in ML, but note that we could easily use other algorithms as well

Data: Predicting Discipline From Abstracts

• For the remainder of this lecture, I will exemplify different approaches to supervised text classification using a data set that contains the title and abstract of scientific articles and their discipline.

science_data <- read_csv("data/science.csv") |> 
  filter(label != "biology" & label != "finance" & label != "mathematics")
science_data |> 
  select(id, label, title, text)

# A tibble: 15,880 × 4
      id label            title                                                                                    text 
   <dbl> <chr>            <chr>                                                                                    <chr>
 1     1 computer science Reconstructing Subject-Specific Effect Maps                                              "Rec…
 2     2 computer science Rotation Invariance Neural Network                                                       "Rot…
 3     5 computer science Comparative study of Discrete Wavelet Transforms and Wavelet Tensor Train decomposition… "Com…
 4     7 physics          On the rotation period and shape of the hyperbolic asteroid 1I/`Oumuamua (2017) U1 from… "On …
 5     8 physics          Adverse effects of polymer coating on heat transport at solid-liquid interface           "Adv…
 6     9 physics          SPH calculations of Mars-scale collisions: the role of the Equation of State, material … "SPH…
 7    11 computer science A global sensitivity analysis and reduced order models for hydraulically-fractured hori… "A g…
 8    12 physics          Role-separating ordering in social dilemmas controlled by topological frustration        "Rol…
 9    13 physics          Dynamics of exciton magnetic polarons in CdMnSe/CdMgSe quantum wells: the effect of sel… "Dyn…
10    14 computer science On Varieties of Ordered Automata                                                         "On …
# ℹ 15,870 more rows

Data: Overview of disciplines

• The data contains articles from computer science, physics, and statistics

• Our goal is to find a neural network archtecture that can label abstracts with these disciplines sufficiently well

science_data |> 
  group_by(label) |> 
  tally() |> 
  ggplot(aes(x = fct_reorder(label, n), y = n)) +
  geom_col(fill = "steelblue") +
  coord_flip() +
  theme_minimal(base_size = 20) +
  labs(x = "", y = "Number of articles")

Creating training and testing data

• For the entire model fitting process, we are going to use the package tidymodels, which nicely intersects with the already known package tidytext

• Here, we can use the functions initial_split to split our data set. The functions training and testing create the actual data sets from the splits.

library(tidymodels)

# Set seed to insure replicability
set.seed(42)

# Create initial split proporations
split <- initial_split(science_data, prop = .90)

# Create training and test data
train_data <- training(split)
test_data <- testing(split)

# Check
tibble(dataset = c("training", "testing"),
       n_songs = c(nrow(train_data), nrow(test_data)))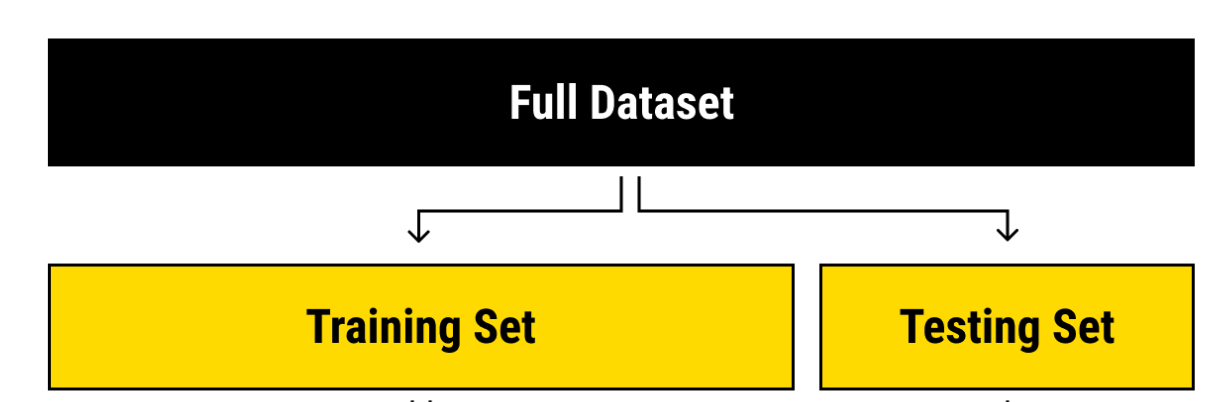

# A tibble: 2 × 2
  dataset  n_songs
  <chr>      <int>
1 training   14292
2 testing     1588

Feature Engineering

• Classic machine learning models require a numerical representation of text (e.g., document-feature matrix)

• They further need the outcome variable that they should predict

• All text-preprocessing steps (e.g., stopword removal, stemming, frequency trimming,etc.) may change the performance, but no clear rules on what works and what does not

• Only solution: Trial and error!

Text Preprocessing with TidyText

library(tidytext)

# Text Preprocessing
dfm_train <- train_data |>
  unnest_tokens(word, text) |>                     # <-- Tokenization
  anti_join(stop_words) |>                         # <-- Remove stop words
  group_by(id, word) |>                            # <-- group by text and word
  summarize(n = n()) |>                            # <-- count word frequencies
  cast_dfm(document = id, term = word,  value = n) # <-- create DFM

# Check
dfm_train |> 
  head()

Document-feature matrix of: 6 documents, 48,379 features (99.87% sparse) and 0 docvars.
    features
docs accuracy ad adni aims algorithm alterations alzheimer's amyloid analyses analyzing
   1        1  1    3    1         1           1           2       1        1         1
   2        0  0    0    0         0           0           0       0        0         0
   5        1  0    0    0         0           0           0       0        0         0
   7        0  0    0    0         0           0           0       0        0         0
   8        0  0    0    0         0           0           0       0        0         0
   9        0  0    0    0         0           0           0       0        0         0
[ reached max_nfeat ... 48,369 more features ]

Alternative in tidymodels: Creating A “Recipe”

library(textrecipes)

# Create recipe for text preprocessing
rec <- recipe(label ~ text, data = science_data) |>
  step_tokenize(text, options = list(strip_punct = T, strip_numeric = T)) |>  # <-- Tokenization
  step_stopwords(text, language = "en") |>                                    # <-- Remove stop words
  step_tf(all_predictors())                                                   # <-- Create DFM

# "Bake" (check) based on recipe to see text preprocessing
rec |> 
  prep(train_data) |>
  bake(new_data=NULL)

# A tibble: 14,292 × 44,333
   label  tf_text__aster tf_text__b tf_text__c tf_text__catalogue tf_text__d tf_text__e tf_text__f tf_text__g tf_text__h
   <fct>           <int>      <int>      <int>              <int>      <int>      <int>      <int>      <int>      <int>
 1 stati…              0          0          0                  0          0          0          0          0          0
 2 physi…              0          0          0                  0          0          0          0          0          0
 3 physi…              0          0          0                  0          0          0          0          0          0
 4 compu…              0          0          0                  0          0          0          0          0          0
 5 compu…              0          0          0                  0          0          0          0          0          0
 6 compu…              0          0          0                  0          1          0          0          0          0
 7 compu…              0          0          0                  0          0          0          0          0          0
 8 physi…              0          0          0                  0          0          0          0          0          0
 9 physi…              0          0          0                  0          0          0          0          0          0
10 compu…              0          0          0                  0          0          0          0          0          0
# ℹ 14,282 more rows
# ℹ 44,323 more variables: tf_text__i <int>, tf_text__j <int>, tf_text__k <int>, tf_text__m <int>, tf_text__n <int>,
#   tf_text__p <int>, tf_text__q <int>, tf_text__r <int>, tf_text__s <int>, tf_text__svd <int>, tf_text__t <int>,
#   tf_text__u <int>, tf_text__v <int>, tf_text__x <int>, tf_text__y <int>, tf_text__z <int>, tf_text_0.0001s <int>,
#   tf_text_0.031mj <int>, tf_text_0.05dex <int>, tf_text_0.12v <int>, tf_text_0.18um <int>, tf_text_0.1c <int>,
#   tf_text_0.1dex <int>, tf_text_0.254r <int>, tf_text_0.2c <int>, tf_text_0.2db <int>, tf_text_0.2l <int>,
#   tf_text_0.2r_ <int>, tf_text_0.3a <int>, tf_text_0.3t_ <int>, tf_text_0.4gyr <int>, tf_text_0.4k <int>, …

Workflow in Tidymodels

• The collection tidymodels contains a variety of packages that facilitates and streamlines machine learning in R

• The basic procedure is the following:

  1. Create a recipe (a formula and all pre-processing steps)
  2. Bake training and testing data using the recipe (not explicitly necesssary)
  3. Create a model function (depending on what type of algorithm should be used)
  4. Bind all together using a workflow
  5. Fit the entire workflow and evaluate performance

Setting up a recipe for our example

# Load specific support library
library(textrecipes)

# Create recipe
rec <- recipe(label ~ text, data = science_data)                  # <-- predict binary_genre by text

Setting up a recipe for our example

# Load specific support library
library(textrecipes)

# Create recipe
rec <- recipe(label ~ text, data = science_data) |>               # <-- predict binary_genre by text
  step_tokenize(text, options = list(strip_punct = T,             # <-- tokenize, remove punctuation
                                     strip_numeric = T))          # <-- remove numbers

Setting up a recipe for our example

# Load specific support library
library(textrecipes)

# Create recipe
rec <- recipe(label ~ text, data = science_data) |>               # <-- predict binary_genre by text
  step_tokenize(text, options = list(strip_punct = T,             # <-- tokenize, remove punctuation
                                     strip_numeric = T)) |>       # <-- remove numbers
  step_stopwords(text, language = "en") |>                        # <-- remove stopwords                 
  step_tokenfilter(text, min_times = 20, max_tokens = 1000)       # <-- filter out rare words and use only top 1000                         

Setting up a recipe for our example

# Load specific support library
library(textrecipes)

# Create recipe
rec <- recipe(label ~ text, data = science_data) |>               # <-- predict binary_genre by text
  step_tokenize(text, options = list(strip_punct = T,             # <-- tokenize, remove punctuation
                                     strip_numeric = T)) |>       # <-- remove numbers
  step_stopwords(text, language = "en") |>                        # <-- remove stopwords                 
  step_tokenfilter(text, min_times = 20, max_tokens = 1000) |>    # <-- filter out rare words and use only top 1000               
  step_tf(all_predictors())                                       # <-- create document-feature matrix

Setting up a recipe for our example

# Load specific support library
library(textrecipes)

# Create recipe
rec <- recipe(label ~ text, data = science_data) |>               # <-- predict binary_genre by text
  step_tokenize(text, options = list(strip_punct = T,             # <-- tokenize, remove punctuation
                                     strip_numeric = T)) |>       # <-- remove numbers
  step_stopwords(text, language = "en") |>                        # <-- remove stopwords                 
  step_tokenfilter(text, min_times = 20, max_tokens = 1000) |>    # <-- filter out rare words and use only top 1000               
  step_tf(all_predictors())                                       # <-- create document-feature matrix

# Small adaption to the recipe (for SVM and neural networks)
rec_norm <- rec |> 
  step_normalize(all_predictors())    

Theoretical background

• An artificial neural network models the relationship between a set of input signals and an output signal using a model derived from our understanding of the human brain

• Like a brain uses a network of interconnected cells called “neurons” (a) to provide fast learning capabilities, a neural network uses a network of artificial neurons (b) to solves learning tasks

Source: Arthur Arnx/Medium

How does a neural network work?

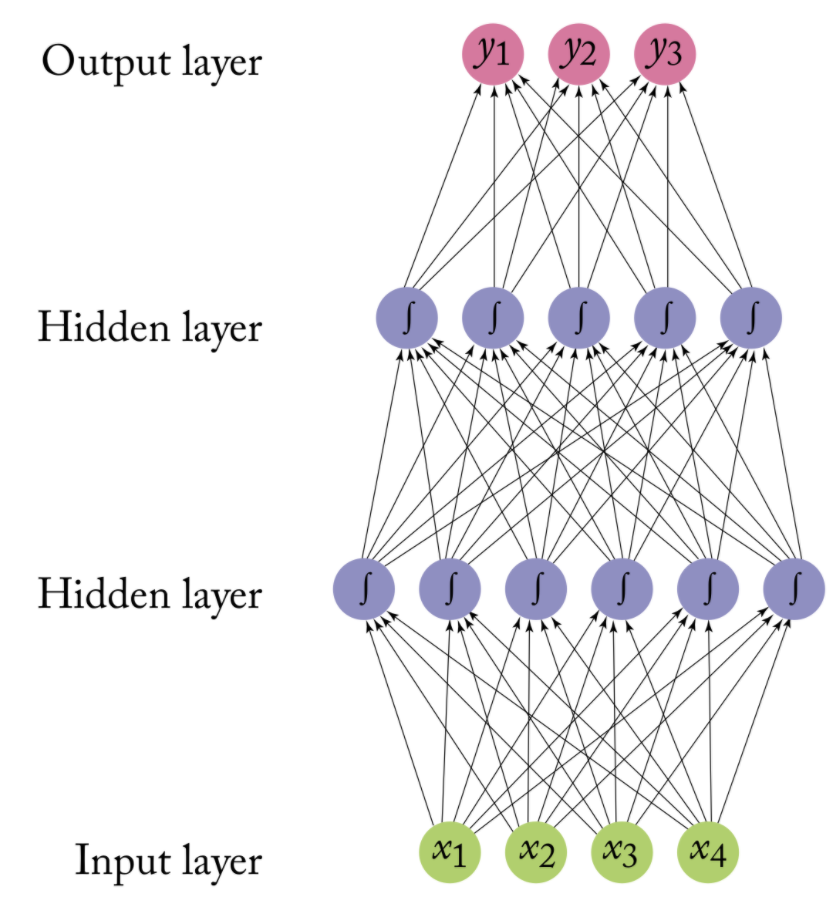
• The operation of an artificial neural network is straightforward:

  • One enters variables as inputs (e.g., features of a text)
  • And after some calculations via different neurons, an output is returned (e.g. the word “politics”)

• Neurons are stacked on top of one another and a neuron of colum n can only be connected to inputs from column n-1 and provide outputs to neurons in column n+1

• In other words, input data are passed through layered transformations until an output is reached

The Neuron as Generalized Linear Model

• First, the value of each input neuron is multiplied by so-called “weight” (w1, w2, w3), which could be regarded as the strength of connection between two neurons

• Second, the neuron adds up the values of every input neuron from the previous column it is connected to (here x1, x2, and x3)

• Third, a bias value may be added (e.g., to regularize the network)

• After all those summations, the neuron finally applies a function called “activation function” to the obtained value

Source: Arthur Arnx/Medium

The activation function

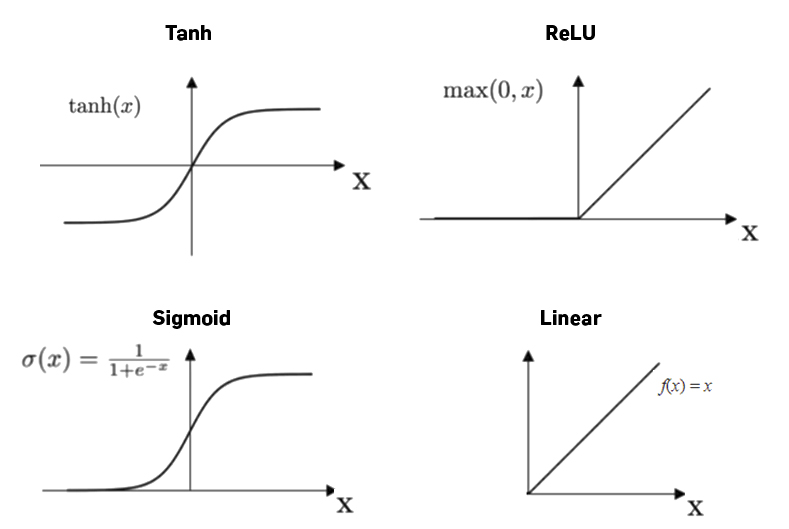
• The activation function serves to turn the total value calculated to a number between 0 and 1

• A threshold then defines at what value the function should “fire” the output to the next neuron (of course this can be probabilistic)

• We can choose from different activation functions; which works best is sometimes hard to tell

Source: AI Wiki

A multilayer Perceptron for our example

How the neural network learns

• In a first try, the neural network randomly sets weights and thus can’t get the right output (except with luck)

• If the random choice was a good one, actual parameters are kept and the next input is given. If the obtained output doesn’t match the desired output, the weights are changed

• To determine which weight is better to modify, a neural network uses backpropagation, which consists of “going back” on the neural network and inspect every connection to check how the output would behave according to a change on the weight

• The learning rate thereby determines the speed a neural network will learn, i.e., how it will modify a weight (e.g., little by little or by bigger steps).

• Learning rate and number of learning cycles (so-called epochs) have to be set manually upfront!

Backpropagation in Detail: Random initialization

Backpropagation in Detail: Costs Function

Backpropagation in Detail: Adjusting weights

What did the neural network learn?

• It is hard to imagine how the network has learned that a certain combination of words corresponds to a certain label.

• In fact, we can only speculate that it might capture certain meaning by co-occurence of words, e.g., that certain words are representing machine learning and machine learning, in turn, is most likely to be within “computer science”

What a neural network might have learned…

What a neural network might have learned…

Fitting an artifical neural network

# For replication purposes
set.seed(42)

# Specify multilayer perceptron
nnet_spec <- 
  mlp(epochs = 400,          # <- times that algorithm will work through train set
      hidden_units = c(6),   # <- nodes in hidden units
      penalty = 0.01,        # <- regularization
      learn_rate = 0.2) |>   # <- shrinkage
  set_engine("brulee") |>    # <- engine = R package
  set_mode("classification")

# Create workflow
ann_workflow <- workflow() |>
  add_recipe(rec_norm) |>    # Use updated recipe with normalization
  add_model(nnet_spec)

Fitting an artifical neural network

# For replication purposes
set.seed(42)

# Specify multilayer perceptron
nnet_spec <- 
  mlp(epochs = 400,          # <- times that algorithm will work through train set
      hidden_units = c(6),   # <- nodes in hidden units
      penalty = 0.01,        # <- regularization
      learn_rate = 0.2) |>   # <- shrinkage
  set_engine("brulee") |>    # <- engine = R package
  set_mode("classification") 

# Create workflow
ann_workflow <- workflow() |>
  add_recipe(rec_norm) |>    # Use updated recipe with normalization
  add_model(nnet_spec)

# Fit model
m_ann <- fit(ann_workflow, train_data)

Predicting labels in the testing data

• We then use the resulting classifier (the neural network) to classify the test data and compare it with the actual labels

# Predict outcome in test data
predict_ann <- predict(m_ann, new_data = test_data) %>%
  bind_cols(test_data) |> 
  mutate(truth = factor(label)) |> 
  select(id, predicted = .pred_class, truth, title)

# Check
predict_ann |> 
 head(n = 4)

# A tibble: 4 × 4
     id predicted        truth            title                                 
  <dbl> <fct>            <fct>            <chr>                                 
1    31 computer science computer science mixup: Beyond Empirical Risk Minimiza…
2    35 computer science computer science Deep Neural Network Optimized to Resi…
3    48 computer science computer science Wehrl Entropy Based Quantification of…
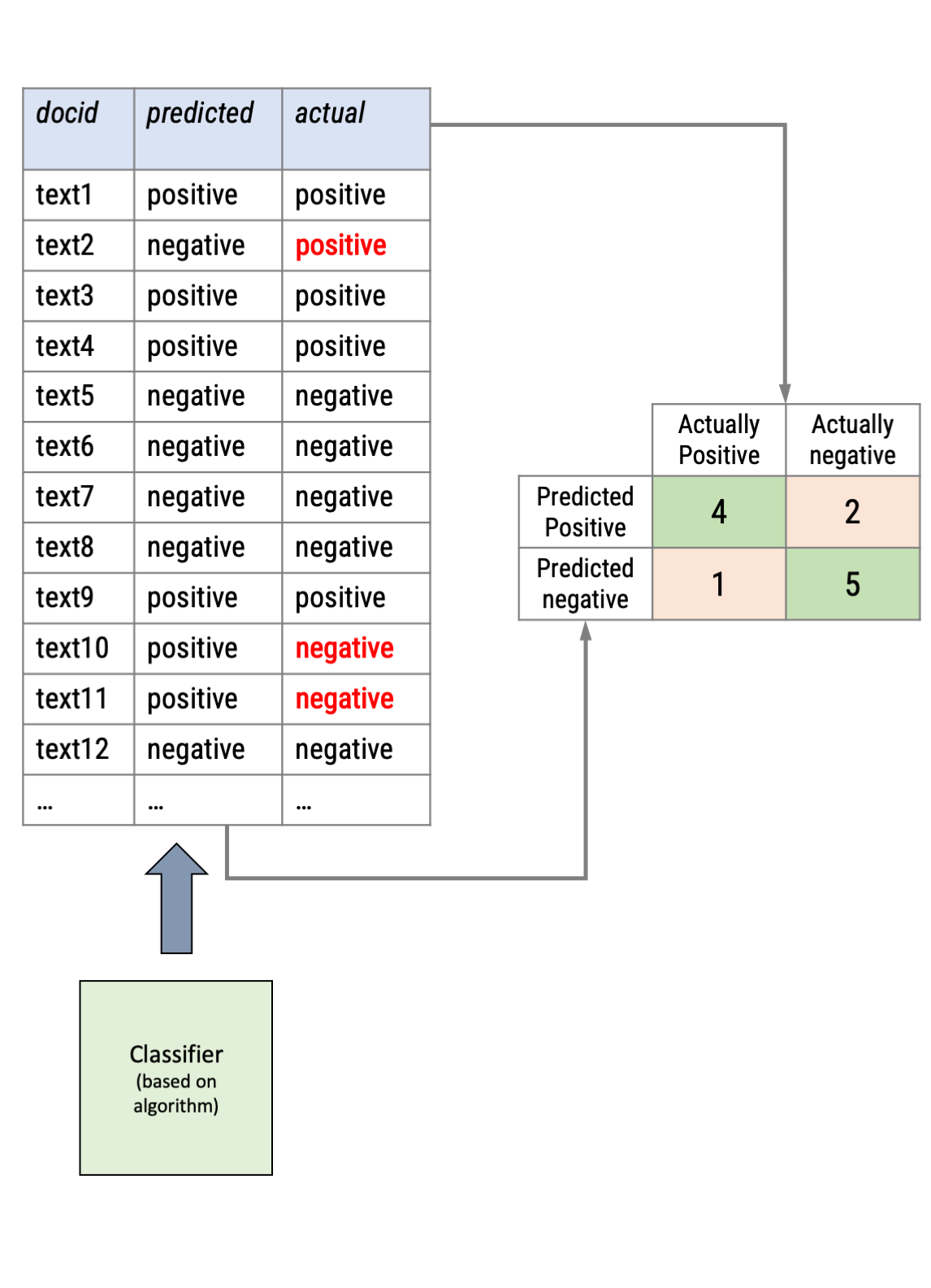
4    55 computer science computer science An Effective Framework for Constructi…

• In tidymodels, we have to define a set of measures that we want to compute based on the predictions in the test set.

# Define a set of performance scores to be computed
class_metrics <- metric_set(accuracy, precision, recall, f_meas)

Validation

• We then can inspect the confusion matrix

• We see here that it does get a lot of articles right, but there are also some false positives and false negatives

# Confusion matrix
predict_ann |> 
  conf_mat(truth = truth, estimate = predicted)

                  Truth
Prediction         computer science physics statistics
  computer science              811      30        105
  physics                        22     539          4
  statistics                     17       1         59

• Based on the performance scores, we see that it actually doesn’t perform bad at all

# Performance score
predict_ann |> 
  class_metrics(truth = truth, estimate = predicted)

# A tibble: 4 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 accuracy  multiclass     0.887
2 precision macro          0.859
3 recall    macro          0.750
4 f_meas    macro          0.778

Fitting a different model (e.g., SVM)

• With tidymodels, we can very easily use a different algorithm.

• Because we already set up a recipe that works with Support Vector Machines, the only thing we have to do is update the workflow and add the new model

library(LiblineaR)

# Updating the workflow
svm_workflow <- workflow() |>
  add_recipe(rec_norm) |>                         # <-- Recipe remains the same!                
  add_model(svm_linear(mode = "classification",   # <-- We just add a new model (e.g Support Vector Machines)
                     engine = "LiblineaR"))

# Fitting the SVM model
m_svm <- fit(svm_workflow, data = train_data)

Comparison of the previous approaches

# Predict test data
predict_svm <- predict(m_svm, new_data=test_data) |> 
  bind_cols(test_data) |> 
  mutate(truth = factor(label)) |> 
  select(id, predicted = .pred_class, truth, title)

# Combine predict data from SVM and neural network
bind_rows(
  # Compute class_metrics for SVM
  predict_svm |> 
    class_metrics(truth=truth, estimate=predicted) |>
    mutate(algorithm = "support vector machines"),
  # Compute class_metrics for NN
  predict_ann |> 
    class_metrics(truth=truth, estimate=predicted) |>
    mutate(algorithm = "neural network")) |> 
  # Plot comparison
  ggplot(aes(x = .metric, y = .estimate, 
             fill = algorithm)) +
  geom_col(position=position_dodge(), alpha=.5) +
  geom_text(aes(label = round(.estimate, 3)), 
            position = position_dodge(width=1)) +
  ylim(0, 1) +
  coord_flip() +
  scale_fill_brewer(palette = "Dark2") +
  theme_minimal(base_size = 18) +
  theme(legend.position = "bottom") +
  labs(y = "Performance Score", x = "", fill = "")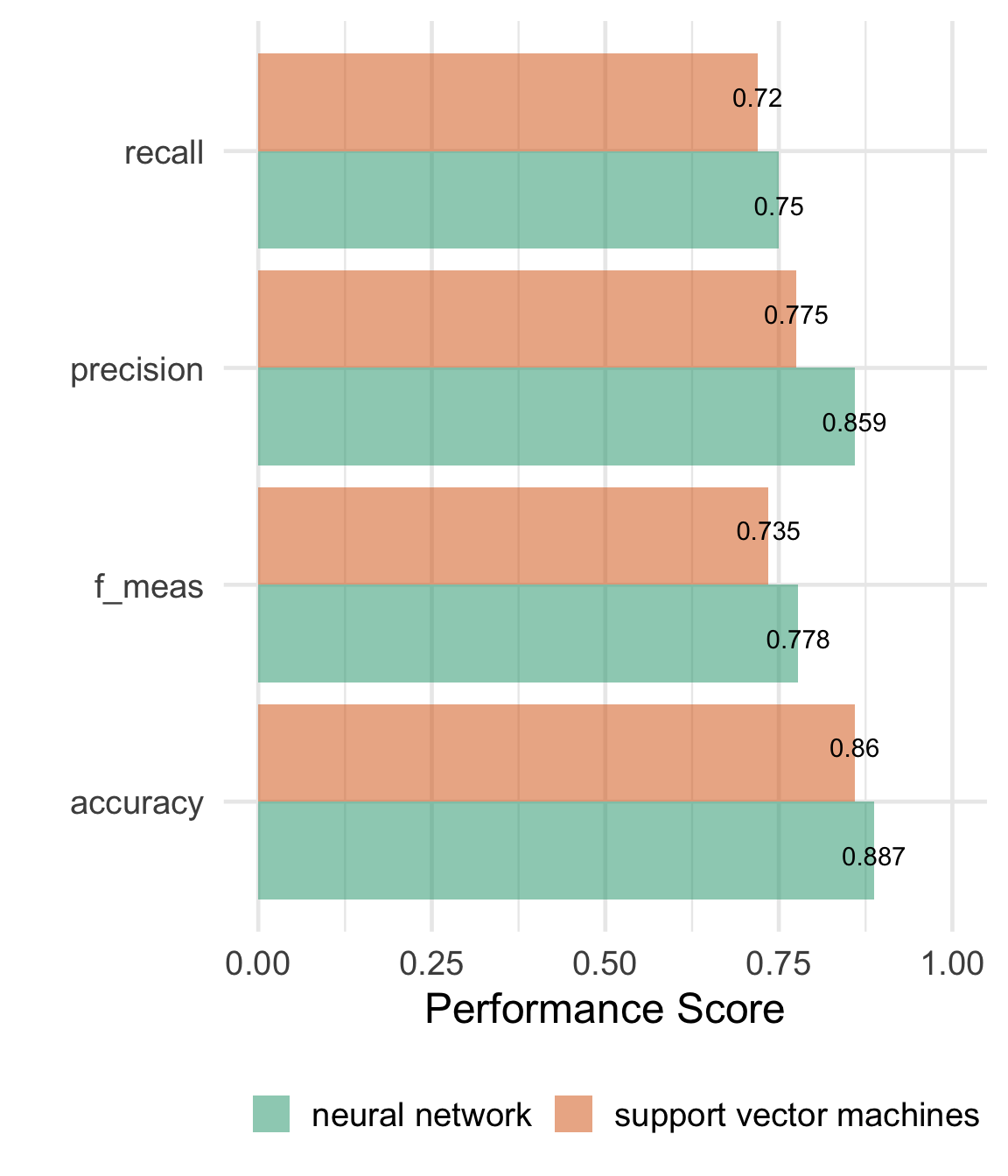

Break (5 Minutes)

Word-Embeddings

More Complex Text Representations

Rember: The initial problem of text analysis

• Computers don’t read text, they only can deal with numbers

• For this reason, so far, we tokenized our texts (e.g., in words) and summarized their frequency across texts to create a document-feature matrix within the bag-of-words model

• Such a text representation has some issues:

  • Treats words as equally important (→ requires removal of noise, stopwords…)
  • Ignores word order and context
  • Results in a sparse matrix (→ computationally expensive)

Alternative: Map words into a vector space

(Static) Word embeddings

• Word embeddings are a “learned” type of word representation that allows words with similar meaning to have a similar representation via a k-dimensional vector space

• The first core idea behind word embeddings is that the meaning of a word can be expressed using a relatively small embedding vector, generally consisting of around 300 numbers which can be interpreted as dimensions of meaning

• The second core idea is that these embedding vectors can be derived by scanning the context of each word in millions and millions of documents.

• This means that words that are used in similar ways in the training data result in similar representations, thereby capturing their similar meaning.

How do we get these “values” for each word?

All word embedding methods learn a real-valued vector representation for a predefined fixed-sized vocabulary from a corpus of text:

1. Via an embedding layer in a neural network designed for a particular downstream task

2. Learning word embeddings using a shallow neural network and context windows (e.g., word2vec)

3. Learning word embeddings by aggregating global word-word co-occurrence matrix (e.g., GloVe)

Pre-trained Word embeddings: GloVe

• GloVe captures global statistical information from a text corpus by looking at word co-occurrences across the entire corpus, not just in local contexts (like neighboring words):

glove_fn = "glove.6B.50d.10k.w2v.txt"
url = glue::glue("https://cssbook.net/d/{glove_fn}")
if (!file.exists(glove_fn)) 
    download.file(url, glove_fn)

# Data wrangling
wv_tibble <- read_delim(glove_fn, skip=1, delim=" ", quote="", 
    col_names = c("word", paste0("d", 1:50)))

# 10 highest scoring words on dimension 1
wv_tibble |> 
  arrange(-d1) |> head()

# A tibble: 6 × 51
  word      d1     d2     d3      d4      d5     d6      d7     d8     d9    d10
  <chr>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>  <dbl>  <dbl>
1 airbus  2.60 -0.536  0.414  0.339  -0.0510  0.848 -0.722  -0.361  0.869 -0.731
2 space…  2.52  0.744  1.66   0.0591 -0.252  -0.243 -0.594  -0.417  0.460 -0.124
3 fiat    2.29 -1.15   0.488  0.518   0.312  -0.132  0.0520 -0.661 -0.859  0.263
4 naples  2.27 -0.106 -1.27  -0.0932 -0.437  -1.18  -0.0858  0.469 -1.08  -0.549
5 di      2.24 -0.603 -1.47   0.354   0.244  -1.09   0.357  -0.331 -0.564  0.428
6 planes  2.20 -0.831  1.34  -0.348  -0.209  -0.282 -0.824  -0.481  0.211 -0.748
# ℹ 40 more variables: d11 <dbl>, d12 <dbl>, d13 <dbl>, d14 <dbl>, d15 <dbl>,
#   d16 <dbl>, d17 <dbl>, d18 <dbl>, d19 <dbl>, d20 <dbl>, d21 <dbl>,
#   d22 <dbl>, d23 <dbl>, d24 <dbl>, d25 <dbl>, d26 <dbl>, d27 <dbl>,
#   d28 <dbl>, d29 <dbl>, d30 <dbl>, d31 <dbl>, d32 <dbl>, d33 <dbl>,
#   d34 <dbl>, d35 <dbl>, d36 <dbl>, d37 <dbl>, d38 <dbl>, d39 <dbl>,
#   d40 <dbl>, d41 <dbl>, d42 <dbl>, d43 <dbl>, d44 <dbl>, d45 <dbl>,
#   d46 <dbl>, d47 <dbl>, d48 <dbl>, d49 <dbl>, d50 <dbl>

Words in a multidimensional vector space

Similar words have similar characteristics

Multidimensional vector space

Multidimensional vector space

Multidimensional vector space

Similarities between words

With word-embeddings, we can compute similarity scores for word pairs, which proves the “encoding of meaning” in word-embeddings:

wv <- as.matrix(wv_tibble[-1])
rownames(wv) <- wv_tibble$word
wv <- wv / sqrt(rowSums(wv^2))
wvector <- function(wv, word) wv[word,,drop=F]
wv_similar <- function(wv, target, n=5) {
  similarities = wv %*% t(target)
  similarities |>  
    as_tibble(rownames = "word") |> 
    rename(similarity=2) |> 
    arrange(-similarity) |>  
    head(n=n)  
}

wv_similar(wv, wvector(wv, "basketball"))

# A tibble: 5 × 2
  word       similarity
  <chr>           <dbl>
1 basketball      1    
2 football        0.879
3 hockey          0.862
4 baseball        0.861
5 nba             0.838

wv_similar(wv, wvector(wv, "netherlands"))

# A tibble: 5 × 2
  word        similarity
  <chr>            <dbl>
1 netherlands      1    
2 belgium          0.893
3 switzerland      0.821
4 denmark          0.809
5 france           0.789

Similarity of entire sentences or texts

But we can also generalize word embeddings to entire sentences (or even texts):

library(ccsamsterdamR)

# Example sentences
movies <- tibble(sentences = c("This movie is great, I loved it.", 
                               "The film was fantastic, a real treat!",
                               "I did not like this movie, it was not great.",
                               "Today, I went to the cinema and watched a movie",
                               "I had pizza for lunch.",
                               "Sometimes, when I read a book, I get completely lost."))
                     
# Get embeddings from a sentence transformer
movie_embeddings <- hf_embeddings(txt = movies$sentences)

# Each text has now 384 values
movie_embeddings 

# A tibble: 6 × 384
       V1       V2      V3       V4      V5       V6       V7      V8      V9      V10     V11      V12      V13
    <dbl>    <dbl>   <dbl>    <dbl>   <dbl>    <dbl>    <dbl>   <dbl>   <dbl>    <dbl>   <dbl>    <dbl>    <dbl>
1 -0.0875 -0.0156  -0.0380 -0.0586  -0.0842  0.0164  -0.0222   0.0451  0.0449 -0.00546 -0.0115 -0.00166  0.00575
2 -0.0544  0.0381  -0.0443 -0.0111  -0.0464 -0.00760 -0.0523   0.0173 -0.0725 -0.0432   0.0206  0.00903  0.0223 
3 -0.0838  0.0135  -0.0938 -0.0351  -0.0848 -0.0424  -0.00107  0.0537  0.0559 -0.0729   0.0153  0.0359   0.0396 
4 -0.0442  0.00655  0.0754 -0.0341   0.0637  0.00674  0.0993  -0.0369  0.0752 -0.0405   0.0222  0.0284  -0.0243 
5 -0.0257  0.0440   0.0407  0.00391 -0.0818 -0.0621   0.0836  -0.0138 -0.101  -0.0757   0.0882 -0.0530   0.0351 
6  0.0207  0.00907 -0.0388  0.0717   0.0419  0.0419   0.0267   0.0685  0.0879 -0.0125   0.0281  0.0503  -0.0437 
# ℹ 371 more variables: V14 <dbl>, V15 <dbl>, V16 <dbl>, V17 <dbl>, V18 <dbl>, V19 <dbl>, V20 <dbl>, V21 <dbl>,
#   V22 <dbl>, V23 <dbl>, V24 <dbl>, V25 <dbl>, V26 <dbl>, V27 <dbl>, V28 <dbl>, V29 <dbl>, V30 <dbl>, V31 <dbl>,
#   V32 <dbl>, V33 <dbl>, V34 <dbl>, V35 <dbl>, V36 <dbl>, V37 <dbl>, V38 <dbl>, V39 <dbl>, V40 <dbl>, V41 <dbl>,
#   V42 <dbl>, V43 <dbl>, V44 <dbl>, V45 <dbl>, V46 <dbl>, V47 <dbl>, V48 <dbl>, V49 <dbl>, V50 <dbl>, V51 <dbl>,
#   V52 <dbl>, V53 <dbl>, V54 <dbl>, V55 <dbl>, V56 <dbl>, V57 <dbl>, V58 <dbl>, V59 <dbl>, V60 <dbl>, V61 <dbl>,
#   V62 <dbl>, V63 <dbl>, V64 <dbl>, V65 <dbl>, V66 <dbl>, V67 <dbl>, V68 <dbl>, V69 <dbl>, V70 <dbl>, V71 <dbl>,
#   V72 <dbl>, V73 <dbl>, V74 <dbl>, V75 <dbl>, V76 <dbl>, V77 <dbl>, V78 <dbl>, V79 <dbl>, V80 <dbl>, V81 <dbl>, …

The subtle similarity of some texts in the example

• We can see that text 2 is most similar to text 1: Both express a very similar sentiment, just with different words (“great” ≈ “fantastic”; “I loved it” ≈ “A real treat”)

• Text 2 is still similar to text 3 (after all it is about movies), but less so compared to text 1 (“fantastic” is the opposite of “not great”)

• Text 4 still shares similarities (the context is the cinema/watching movies), but text 5 is very different as it doesn’t contain similar words and is not about similar things (except “I”).

• Text 5 is very dissimilar to the others.

# Similarity between 2nd and the other sentences
movies |> 
  mutate(similarity = as.matrix(movie_embeddings) %*% t(as.matrix(movie_embeddings)[2,, drop = F])) |> 
  arrange(-similarity)

# A tibble: 6 × 2
  sentences                                             similarity[,1]
  <chr>                                                          <dbl>
1 The film was fantastic, a real treat!                         1.00  
2 This movie is great, I loved it.                              0.646 
3 I did not like this movie, it was not great.                  0.513 
4 Today, I went to the cinema and watched a movie               0.372 
5 I had pizza for lunch.                                        0.132 
6 Sometimes, when I read a book, I get completely lost.         0.0939

Doing analysis with word-embedding themselves

• Based on vector-based computations, we can analyse semantic relationships

• This is a quite common approach by now in research on gender and other types of stereotypes

Source: https://developers.google.com

Example from the literature: Gender-Stereotypes

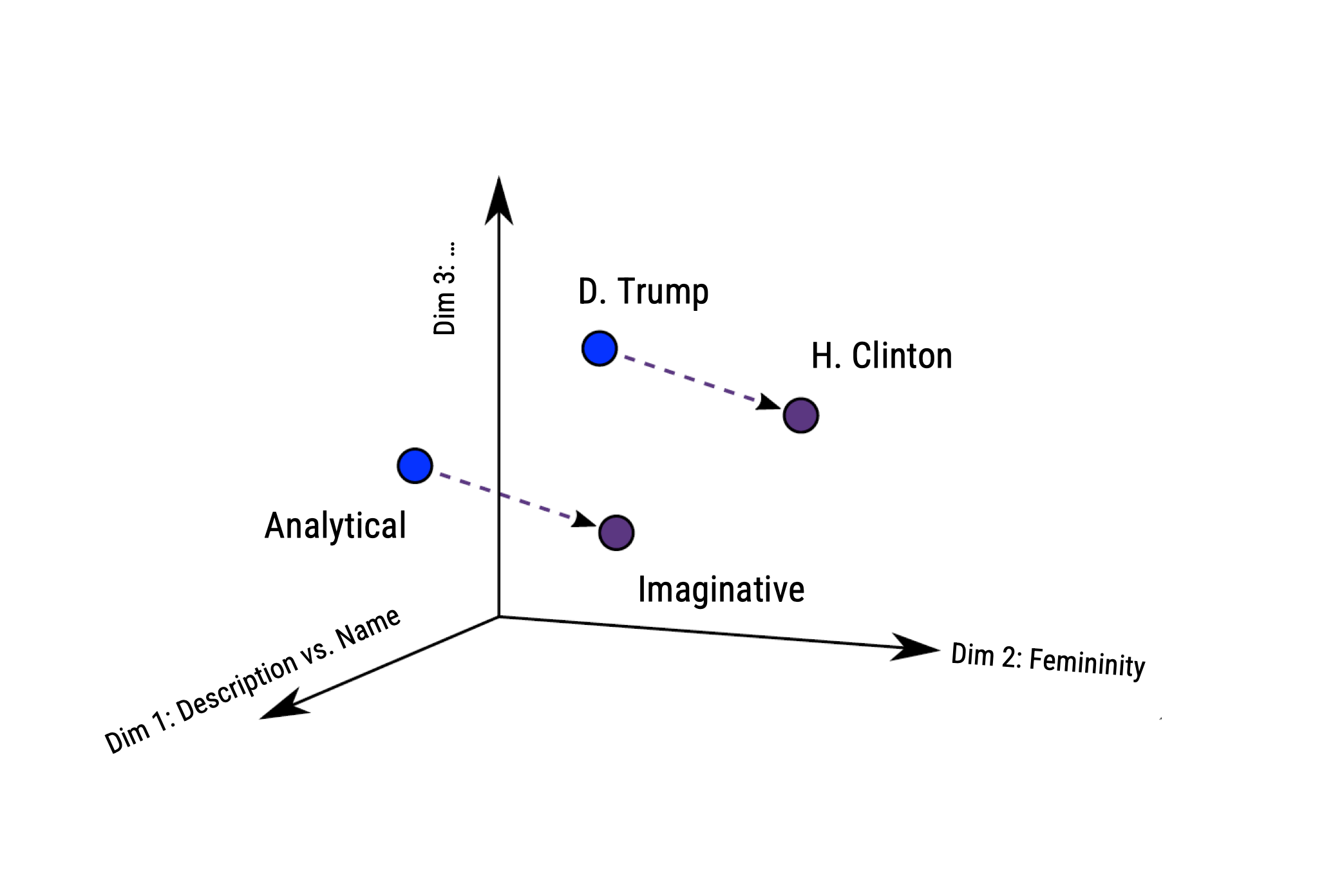• Andrich et al. (2023) examine stereotypical traits in portrayals of 1,095 U.S. politicians.

• Analyzed 5 million U.S. news stories published from 2010 to 2020 to study gender-linked (feminine, masculine) and political (leadership, competence, integrity, empathy) traits

• Methodologically, they estimated word embeddings using the Continuous Bag of Words (CBOW) model, meaning that a target word (e.g., honest) is predicted from its context (e.g., Who thinks President Trump is [target word]?)

• Bias can thus be identified if e.g., gender-neutral words (e.g., competent) are closer to words that represent one gender (e.g., donald_trump) than to words that represent the opposite gender (e.g., hillary_clinton).

Results

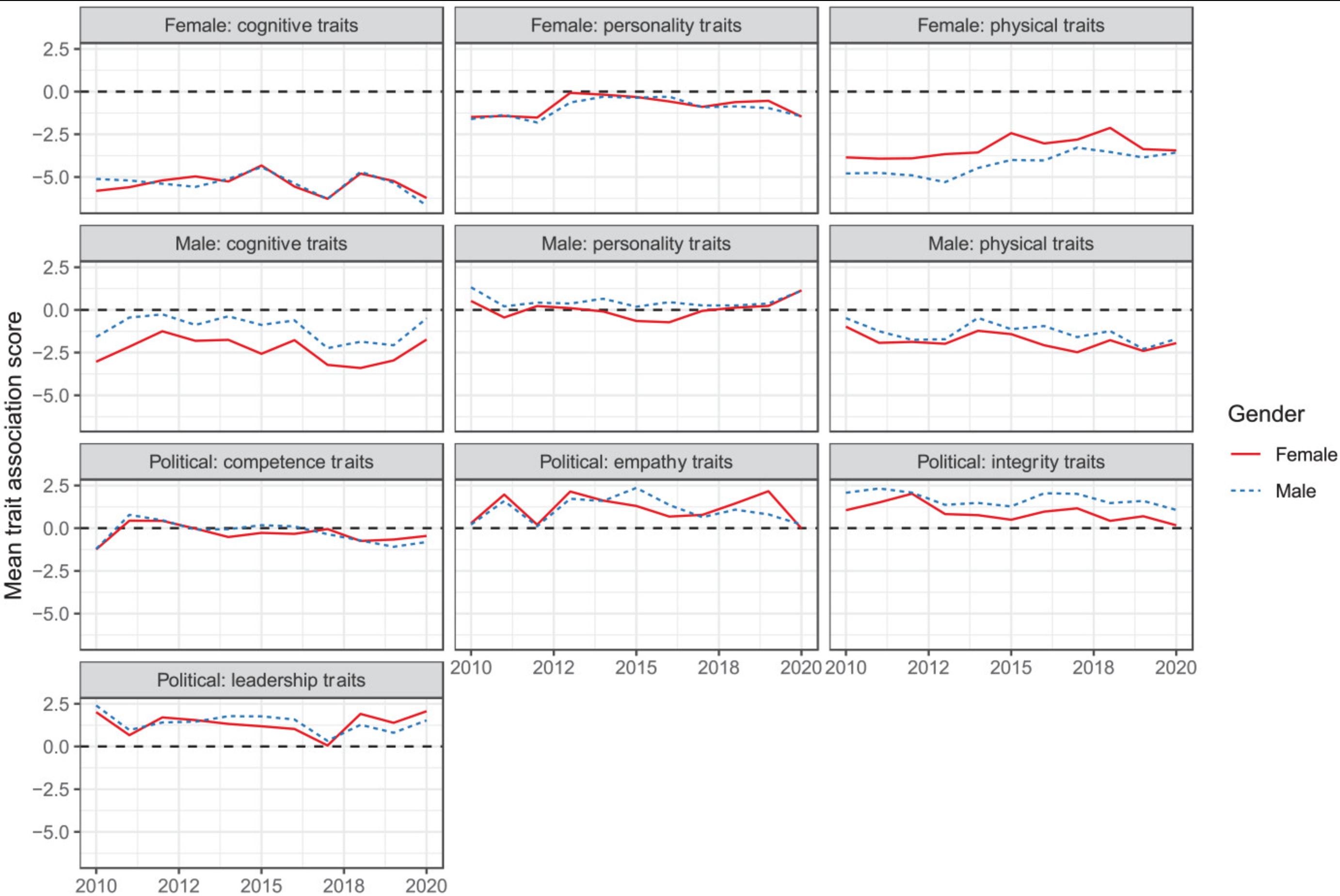
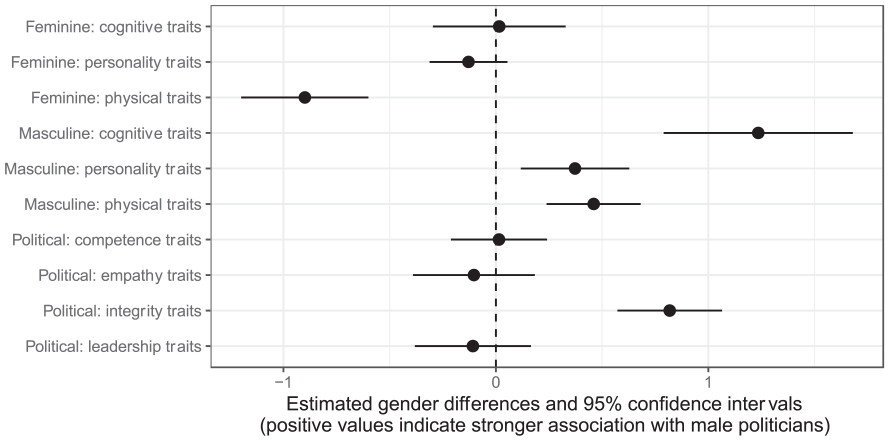
• All three masculine traits were more strongly associated with male politicians.

• In contrast, only the feminine physical traits were more strongly associated with female politicians.

• Differences remained stable across time.

Text Classification with Word-Embeddings

Improving Prediction by Using Word-Embeddings as Input Features

Word Embeddings as Input to classic ML models

• Word, sentence, or text embedding vectors can then be used as features in further text analysis tasks

• Think about the example we just investigated: The sentence embeddings did capture some difference between:

  • “The film was fantastic, a real treat!” (positive)
  • “I did not like this moive, it was not great.” (negative)

• Approaches from the last lecture (classic machine learning) would have a hard time to detect the negation “not great”.

• Yet, bear in mind: We do not actually know what the 100+ (often >300) dimensions actually mean (→ we cannot look under the hood later!)

Text classification with Word-Embeddings

Fitting a neural network on word-embeddings

• To fit a neural network based on static word-embeddings (e.g., GloVe), we only need to adapt the recipe.

• Here, we do not need to engage in much preprocessing at all:

# Load GloVe embeddings (50-dimensional)
wv_tibble <- readr::read_delim("slides/GloVe 6B/glove.6B.300d.txt", 
                               skip=1, delim=" ", quote="", col_names = c("word", paste0("d", 1:100)))

# Set up the recipe for text preprocessing with GloVe embeddings
text_rec <- recipe(label ~ text, data = science_data) |> 
  step_tokenize(text) |> 
  step_word_embeddings(text, embeddings = wv_tibble, aggregation = "mean") # <-- Here, I am adding the word-embeddings

# Define the MLP model specification
mlp_spec <-
  mlp(epochs = 400,          # <- times that algorithm will work through train set
      hidden_units = c(6),   # <- nodes in hidden units
      penalty = 0.01,        # <- regularization
      learn_rate = 0.2) |>   # <- shrinkage
  set_engine("brulee") |>    # <-- engine = R package
  set_mode("classification")

# Create workflow
mlp_wflow <- workflow()  |> 
  add_recipe(text_rec) |> 
  add_model(mlp_spec)

# Fit the workflow on the training data
mlp_fit <- mlp_wflow |> 
  fit(data = train_data)

Comparison with the two previous approaches

Fine-tuning preprocessing and hyperparameter

• You may have noticed that I always set some hyperparameter in all of the models

• There is no clear rule of how to set these parameters and their influence on performance is often unknown

• We have to simply try out whether a neural network needs more than one hidden layer or how many nodes make sense, what learning rate works best, etc.

• Good machine learning practice is to conduct a so-called grid-search, i.e. systematically run combinations of different specifications (but computationally expensive!!!)

Hvitfeld & Silge (2021)

Grid search for best neural network architecture

# First, we update our model specification
mlp_spec <- mlp(hidden_units = tune(),   # <-- instead of fixed numbers, we set it to "tune"
                penalty = tune(), 
                epochs = tune(), 
                learn_rate = tune()) |> 
  set_engine("brulee", trace = 0) |>  
  set_mode("classification")

Grid Search: Setting specific parameters

# First, we update our model specification
mlp_spec <- mlp(hidden_units = tune(),   # <-- instead of fixed numbers, we set it to "tune"
                penalty = tune(), 
                epochs = tune(), 
                learn_rate = tune()) |> 
  set_engine("brulee", trace = 0) |>  
  set_mode("classification")
  
# Estract "dials" for parameter tuning
mlp_param <- extract_parameter_set_dials(mlp_spec)

# Simple combinatorial design
mlp_param |> grid_regular(levels = c(hidden_units = 2, penalty = 2, epochs = 2, learn_rate = 2)) 

# A tibble: 16 × 4
   hidden_units      penalty epochs learn_rate
          <int>        <dbl>  <int>      <dbl>
 1            1 0.0000000001      5      0.001
 2           10 0.0000000001      5      0.001
 3            1 1                 5      0.001
 4           10 1                 5      0.001
 5            1 0.0000000001    500      0.001
 6           10 0.0000000001    500      0.001
 7            1 1               500      0.001
 8           10 1               500      0.001
 9            1 0.0000000001      5      0.316
10           10 0.0000000001      5      0.316
11            1 1                 5      0.316
12           10 1                 5      0.316
13            1 0.0000000001    500      0.316
14           10 0.0000000001    500      0.316
15            1 1               500      0.316
16           10 1               500      0.316

Running the Grid Search

# Combine the recipe and model into a workflow
mlp_wflow <- workflow() %>%
  add_recipe(text_rec) %>%
  add_model(mlp_spec)

# Set workflow with "dials"
mlp_param <- mlp_wflow  |>  
  extract_parameter_set_dials() |> 
  update(epochs = epochs(c(100, 400)),
         hidden_units = hidden_units(c(12, 64)),
         penalty = penalty(c(-10, -1)),
         learn_rate = learn_rate(range = c(-10, -1), trans = transform_log10()))

# Set metric of interest
acc <- metric_set(accuracy)

# Define resampling strategy
twofold <- vfold_cv(train_data, v = 2) 

# Run the tuning process
mlp_reg_tune <- mlp_wflow  |> 
  tune_grid(
    resamples = twofold,
    grid = mlp_param  |>  
      grid_regular(levels = c(hidden_units = 2, penalty = 2,   # <-- here, we set specific combination of parameters
                              epochs = 2, learn_rate = 2)),    #     instead, we could also use the `grid_random()`function 
    metrics = acc
  )

Evaluation

• The result of this tuning grid search is a table that shows the best combinations of parameters in descending order

• We can see here that 64 nodes, a very low penalty, a learning rate of 0.1 provides the best performance.

best_fit <- show_best(mlp_reg_tune, n = 48) |> 
  select(-.estimator, -.config, -.metric) |> 
  rename(accuracy = mean)
best_fit

# A tibble: 16 × 7
   hidden_units      penalty epochs   learn_rate accuracy     n  std_err
          <int>        <dbl>  <int>        <dbl>    <dbl> <int>    <dbl>
 1           64 0.0000000001    400 0.1             0.856     2 0.00406 
 2           64 0.0000000001    100 0.1             0.856     2 0.000980
 3           12 0.0000000001    100 0.1             0.854     2 0.00406 
 4           64 0.1             400 0.1             0.784     2 0.00245 
 5           12 0.1             100 0.1             0.783     2 0.00287 
 6           12 0.1             400 0.1             0.782     2 0.00357 
 7           64 0.1             100 0.1             0.781     2 0.00371 
 8           12 0.0000000001    400 0.1             0.563     2 0.295   
 9           64 0.0000000001    400 0.0000000001    0.542     2 0.00154 
10           64 0.1             400 0.0000000001    0.435     2 0.106   
11           12 0.0000000001    100 0.0000000001    0.376     2 0.0277  
12           64 0.0000000001    100 0.0000000001    0.328     2 0.216   
13           12 0.0000000001    400 0.0000000001    0.327     2 0.216   
14           12 0.1             400 0.0000000001    0.230     2 0.119   
15           12 0.1             100 0.0000000001    0.228     2 0.120   
16           64 0.1             100 0.0000000001    0.110     2 0.00126 

Evaluation

• The effect of parameters becomes even more clear, when we visualize the grid search:

options(scipen = 999)
autoplot(mlp_reg_tune)

Fitting the best model

mlp_best <-
  mlp(epochs = 400,           # <- times that algorithm will work through train set
      hidden_units = c(64),   # <- nodes in hidden units
      penalty = 0.001,        # <- regularization
      learn_rate = 0.1) |>    # <- shrinkage
  set_engine("brulee") |>     # <-- engine = R package
  set_mode("classification")

# Create workflow
mlp_wflow_best <- workflow()  |> 
  add_recipe(text_rec) |> 
  add_model(mlp_best)

# Fit the workflow on the training data
mlp_fit_best <- mlp_wflow_best |> 
  fit(data = train_data)

# Make predictions and evaluate on the test set
predictions_best <- predict(mlp_fit_best, new_data = test_data) %>%
  bind_cols(test_data) |> 
  mutate(label = factor(label))

predictions_best |> 
 class_metrics(truth = label, estimate = .pred_class)

# A tibble: 4 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 accuracy  multiclass     0.869
2 precision macro          0.826
3 recall    macro          0.716
4 f_meas    macro          0.739

Comparison with other approaches

General Drivers of model performance

1. Task difficulty

2. Amount of training data

3. Choice of features (n-grams, lemmata, etc)

4. Text preprocessing (e.g., exclude or include stopwords?)

5. Representation of text (tf, tf-idf, word-embedding)

6. Tuning of algorithm (what we just did in the grid search)

Impact of text preprocessing on performance?

• Scharkow ran a simple simulation study in which he systematically varied text preprocessing

• The classifier was always Naive Bayes, below we see the average difference in performance

Validity of different approaches

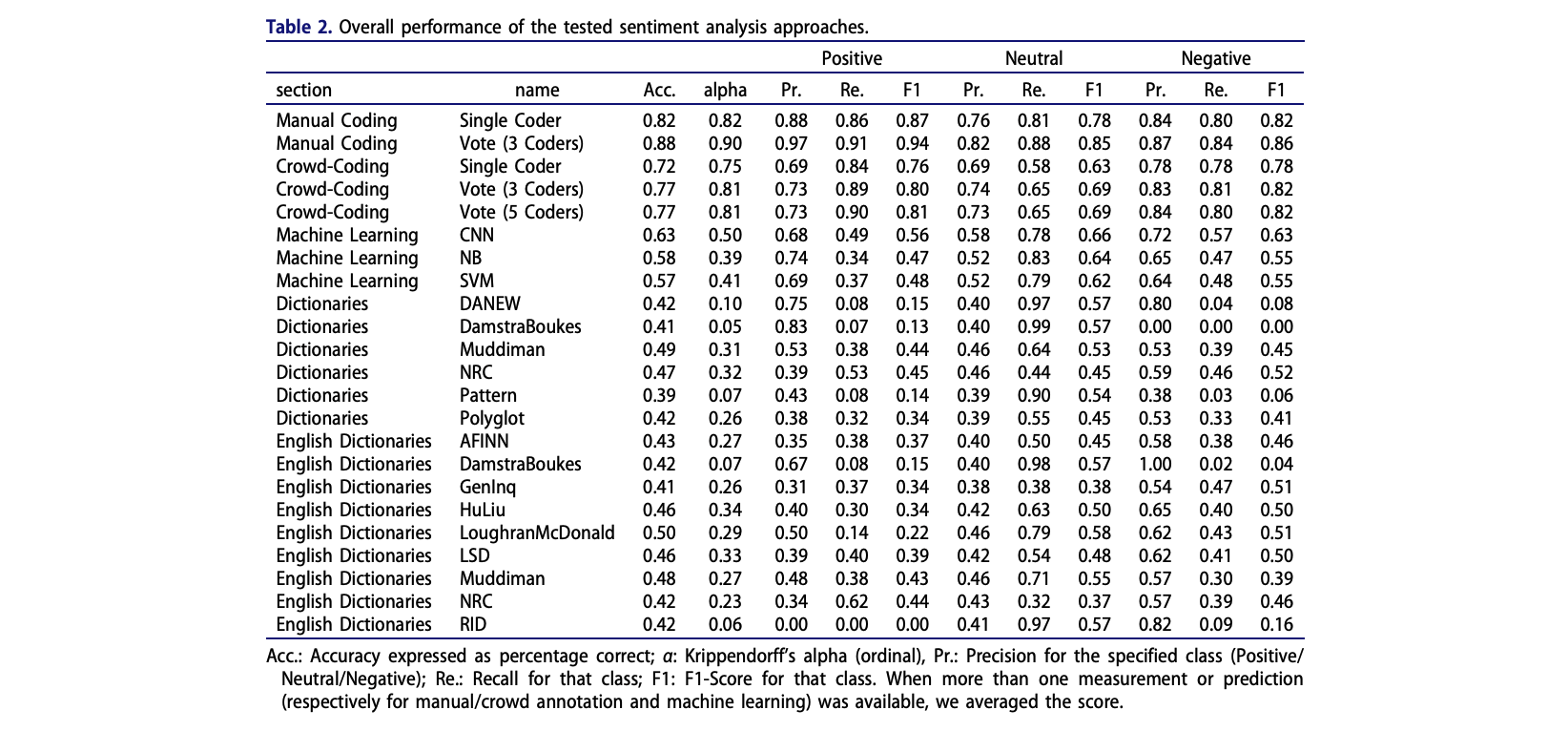
• Van Atteveldt et al. (2021) re-analysised data reported in Boukes et al. (2020) to understand the validity of different text classification approaches for sentiment analysis

• The data included news from a total of ten newspapers and five websites published between February 1 and July 7, 2015:

  • three quality newspapers (NRC Handelsblad, Trouw, de Volkskrant)
  • a financial newspaper (Financieel Dagblad)
  • three popular newspapers (Algemeen Dagblad, Metro, De Telegraaf)
  • three regional outlets (Dagblad van het Noorden, de Gelderlander, Noordhollands Dagblad)

Main results

Examples from the literature

How Machine Learning is used in Communication Science

Example 1: Incivility in Facebook comments

• Su et al. (2018) examined the extent and patterns of incivility in the comment sections of 42 US news outlets’ Facebook pages in 2015–2016

• News source outlets included

  • National-news outlets (e.g., ABC, CBS, CNN…)
  • Local-new outlets (e.g., The Denver Post, San Francisco Chronicle…)
  • Conservative and liberal partisan news outlets (e.g., Breitbart, The Daily Show…)

• Implemented a combination of manual coding and supervised machine learning to code:

  • Civility
  • Interpersonal rudeness
  • Personal rudeness
  • Impersonal extreme incivility
  • Personal extreme incivility

Results: Overall differences

Example 2: Electoral news sharing in Mexico

• de León et al. (2021) explored how elections transform news sharing behaviour on Facebook

• They investigated changes in news coverage and news sharing behaviour on Facebook

  • by comparing election and routine periods, and
  • by addressing the ‘news gap’ between preferences of journalists and news consumers on social media.

• Employed a novel data set of news articles (N = 83,054) in Mexico

• First coded 2,000 articles manually into topics (Politics, Crime and Disasters, Culture and Entertainment, Economic and Business, Sports, and Other), then used support vector machines to classify the rest

Results

• During periods of heightened political activity, both the publication and dissemination of political news increases

• The gap between the news choices of journalists and consumers narrows, and increased political news sharing leading to a decrease in the sharing of other news.

Summary, Conclusion, and Outlook

Next week, we reach the present!

Machine Learning Text Classification Pipeline

Machine Learning Text Classification Pipeline

General considerations

• Machine learning in the social sciences generally used to solve an engineering problem

• Output of Machine Learning is input for “actual” statistical model (e.g., we classify text, but run an analysis of variance with the output)

• Ethical concerns

  • Is it okay to use a model we can’t possibly understand (e.g., SVM, neural networks)?

  • If they lead to false positives or false negatives, which in turn discriminate someone or lead to bias, it is difficult to find the source and denote responsibility

• We always need to validate model on unseen and representative test data!

• Think before you run models or you will waste a lot of computational resources

Conclusion and outlook

• Classic machine learning is a useful tool for generalizing from a sample

• It is very useful to reduce the amount of manual coding needed

• Word-Embeddings are a dense representation of text that can improve speed and performance of standard ML approaches

• That said, the field has moved on and innovations are fast-paced these days:

  • Transfer Learning, Attention, Self-Attention…. (Next week!!!)

Thank you for your attention!

Required Reading

van Atteveldt, W., van der Velden, M. A. C. G., & Boukes, M.. (2021). The Validity of Sentiment Analysis: Comparing Manual Annotation, Crowd-Coding, Dictionary Approaches, and Machine Learning Algorithms. Communication Methods and Measures, (15)2, 121-140, https://doi.org/10.1080/19312458.2020.1869198

Su, L. Y.-F., Xenos, M. A., Rose, K. M., Wirz, C., Scheufele, D. A., & Brossard, D. (2018). Uncivil and personal? Comparing patterns of incivility in comments on the Facebook pages of news outlets. New Media & Society, 20(10), 3678–3699. https://doi.org/10.1177/1461444818757205

(available on Canvas)

References

• Boumans, J. W., & Trilling, D. (2016). Taking stock of the toolkit: An overview of relevant automated content analysis approaches and techniques for digital journalism scholars. Digital journalism, 4(1), 8-23.

• de León, E., Vermeer, S. & Trilling, D. (2023). Electoral news sharing: a study of changes in news coverage and Facebook sharing behaviour during the 2018 Mexican elections. Information, Communication & Society, 26(6), 1193-1209. https://doi.org/10.1080/1369118X.2021.1994629

• Hvitfeld, E. & Silge, J. (2021). Supervised Machine Learning for Text Analysis in R. CRC Press. https://smltar.com/

• Lantz, B. (2013). Machine learning in R. Packt Publishing Ltd.

• Scharkow, M. (2013). Thematic content analysis using supervised machine learning: An empirical evaluation using german online news. Quality & Quantity, 47(2), 761–773. https://doi.org/10.1007/s11135-011-9545-7

• Su, L. Y.-F., Xenos, M. A., Rose, K. M., Wirz, C., Scheufele, D. A., & Brossard, D. (2018). Uncivil and personal? Comparing patterns of incivility in comments on the Facebook pages of news outlets. New Media & Society, 20(10), 3678–3699. https://doi.org/10.1177/1461444818757205

• van Atteveldt, W., van der Velden, M. A. C. G., & Boukes, M.. (2021). The Validity of Sentiment Analysis: Comparing Manual Annotation, Crowd-Coding, Dictionary Approaches, and Machine Learning Algorithms. Communication Methods and Measures, (15)2, 121-140, https://doi.org/10.1080/19312458.2020.1869198

Example Exam Question (Multiple Choice)

Van Atteveldt and colleagues (2020) tested the validity of various automated text analysis approaches. What was their main result?

A. English dictionaries performed better than Dutch dictionaries in classifying the sentiment of Dutch news paper headlines.

B. Dictionary approaches were as good as machine learning approaches in classifying the sentiment of Dutch news paper headlines.

C. Of all automated approaches, supervised machine learning approaches performed the best in classifying the sentiment of Dutch news paper headlines.

D. Manual coding and supervised machine learning approaches performed similarly well in classifying the sentiment of Dutch news paper headlines.

Example Exam Question (Multiple Choice)

Van Atteveldt and colleagues (2020) tested the validity of various automated text analysis approaches. What was their main result?

A. English dictionaries performed better than Dutch dictionaries in classifying the sentiment of Dutch news paper headlines.

B. Dictionary approaches were as good as machine learning approaches in classifying the sentiment of Dutch news paper headlines.

C. Of all automated approaches, supervised machine learning approaches performed the best in classifying the sentiment of Dutch news paper headlines.

D. Manual coding and supervised machine learning approaches performed similarly well in classifying the sentiment of Dutch news paper headlines.

Example Exam Question (Multiple Choice)

How are word embeddings learned?

A. By assigning random numerical values to each word

B. By analyzing the pronunciation of words

C. By scanning the context of each word in a large corpus of documents

D. By counting the frequency of words in a given text

Example Exam Question (Multiple Choice)

How are word embeddings learned?

A. By assigning random numerical values to each word

B. By analyzing the pronunciation of words

C. By scanning the context of each word in a large corpus of documents

D. By counting the frequency of words in a given text

Example Exam Question (Open Format)

Describe the typical process used in supervised text classification.

Any supervised machine learning procedure to analyze text usually contains at least 4 steps:

1. One has to manually code a small set of documents for whatever variable(s) you care about (e.g., topics, sentiment, source,…).

2. One has to train a machine learning model on the hand-coded /gold-standard data, using the variable as the outcome of interest and the text features of the documents as the predictors.

3. One has to evaluate the effectiveness of the machine learning model via cross-validation. This means one has to test the model test on new (held-out) data.

4. Once one has trained a model with sufficient predictive accuracy, precision and recall, one can apply the model to more documents that have never been hand-coded or use it for the purpose it was designed for (e.g., a spam filter detection software)